题目内容
已知函数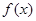 是定义在
是定义在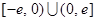 上的奇函数,当
上的奇函数,当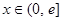 时,有
时,有 (其中
(其中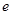 为自然对数的底,
为自然对数的底,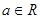 ).
).
(1)求函数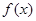 的解析式;
的解析式;
(2)设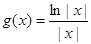 ,
,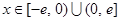 ,求证:当
,求证:当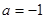 时,
时,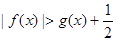 ;
;
(3)试问:是否存在实数 ,使得当
,使得当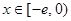 时,
时,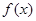 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(1)
(2)构造函数利用函数的最小值大于另一个函数的最大值来证明成立。
(3)当 时,函数
时,函数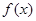 在区间
在区间 上的最小值是3
上的最小值是3
解析试题分析:解:(1)当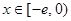 时,
时, ,
,
则 ,
,
又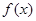 是奇函数,
是奇函数,
所以 ,
,
因此, ; 4分
; 4分
(2)证明:令 ,
,
当 时,注意到
时,注意到 ,所以
,所以
 5分
5分
① 当 时,注意到
时,注意到 ,有
,有 ; 6分
; 6分
② 当 时,
时, , 7分
, 7分
故函数 在
在 上是增函数,从而有
上是增函数,从而有 ,
,
所以当 时,有
时,有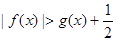 , 8分
, 8分
又因为 是偶函数,故当
是偶函数,故当 时,同样有
时,同样有 ,即
,即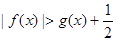 ,
,
综上所述,当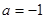 时,有
时,有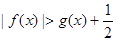 ; 9分
; 9分
(2)证法二:当 时,
时, ,
,
求导得 ,令
,令 得
得 , 5分
, 5分
于是可得当 时,
时, ;
; 时,
时, ,
,
所以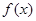 在
在 处取得最大值
处取得最大值 ,所以
,所以 . 6分
. 6分
又记 ,当
,当 时,有
时,有 , 7分
, 7分
求导得 ,当
,当 时,
时, ,
,
所以 在
在 上单调递增,于是
上单调递增,于是 ,
,
所以,在在 上总有
上总有 . 8分
. 8分
注意到 和
和 的偶函数性质,
的偶函数性质,
所以当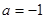 时,有
时,有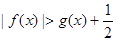 (
(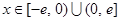 ); 9分
); 9分
(3)当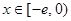 时,
时, ,
,
求导得 ,令
,令 得
得 , 10分
, 10分
① 当 时,
时, ,
,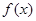 在区间
在区间

练习册系列答案
相关题目
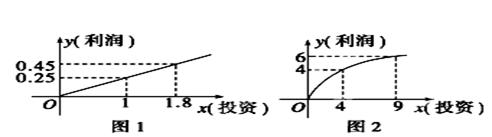
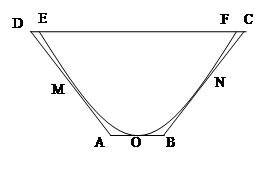
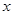 次之间的关系为Z=
次之间的关系为Z=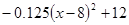 ,1≤
,1≤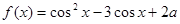 的最大值为6.求
的最大值为6.求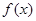 最小值.
最小值. 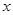 (单位:元/千克)满足关系式y=
(单位:元/千克)满足关系式y=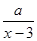 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.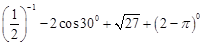 .
. (a为常数),
(a为常数),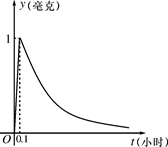
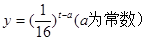 ,如图所示。
,如图所示。