题目内容
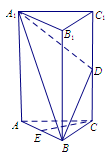
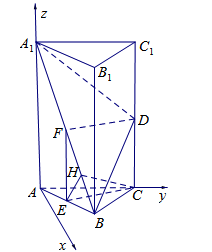
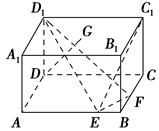
如图,在三棱柱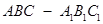 中,△
中,△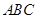 是边长为
是边长为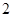 的等边三角形,
的等边三角形,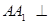 平面
平面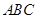 ,
,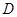 ,
,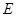 分别是
分别是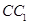 ,
,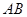 的中点.
的中点.
(1)求证: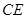 ∥平面
∥平面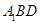 ;
;
(2)若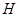 为
为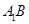 上的动点,当
上的动点,当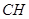 与平面
与平面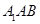 所成最大角的正切值为
所成最大角的正切值为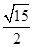 时,求平面
时,求平面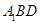 与平面
与平面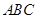 所成二面角(锐角)的余弦值.
所成二面角(锐角)的余弦值.
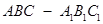 中,△
中,△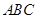 是边长为
是边长为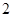 的等边三角形,
的等边三角形, 平面
平面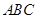 ,
,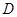 ,
,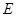 分别是
分别是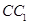 ,
,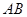 的中点.
的中点. 
(1)求证:
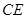 ∥平面
∥平面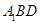 ;
;(2)若
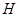 为
为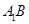 上的动点,当
上的动点,当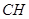 与平面
与平面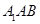 所成最大角的正切值为
所成最大角的正切值为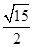 时,求平面
时,求平面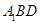 与平面
与平面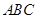 所成二面角(锐角)的余弦值.
所成二面角(锐角)的余弦值.(1)对于线面的平行的证明,关键是证明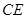 ∥
∥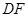 . (2)
. (2)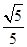
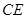 ∥
∥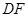 . (2)
. (2)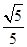
试题分析:(1)证明:取
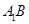 的中点
的中点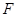 ,连接
,连接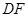 、
、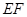 .
. ∵
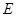 为
为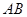 的中点,
的中点,∴
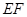 ∥
∥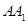 ,且
,且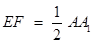 . 1分
. 1分∵
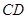 ∥
∥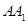 ,且
,且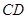
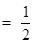
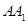 ,∴
,∴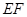 ∥
∥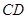 ,
,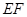
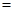
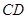 . 2分
. 2分∴四边形
 是平行四边形. ∴
是平行四边形. ∴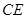 ∥
∥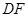 . 3分
. 3分∵
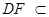 平面
平面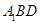 ,
,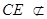 平面
平面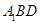 ,∴
,∴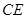 ∥平面
∥平面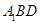 . 4分
. 4分(2)解:∵
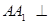 平面
平面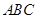 ,
,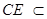 平面
平面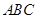 , ∴
, ∴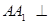
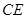 .
. ∵△
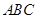 是边长为
是边长为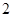 的等边三角形,
的等边三角形,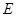 是
是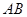 的中点,∴
的中点,∴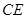
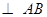 ,
,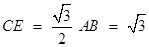 .
. ∵
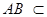 平面
平面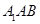 ,
,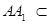 平面
平面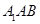 ,
,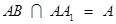 ,∴
,∴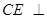 平面
平面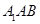 .
.∴
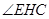 为
为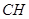 与平面
与平面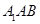 所成的角.
所成的角. ∵
 ,在Rt△
,在Rt△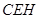 中,
中,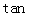
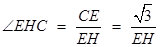 ,
,∴当
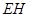 最短时,
最短时,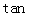
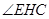 的值最大,则
的值最大,则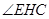 最大.
最大. ∴当
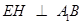 时,
时,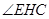 最大. 此时,
最大. 此时,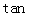
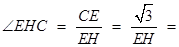
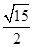 .∴
.∴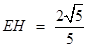 .
.在Rt△
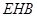 中,
中, .
.∵Rt△
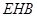 ~Rt△
~Rt△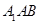 ,
,∴
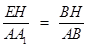 ,即
,即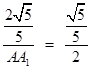 .∴
.∴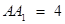 . 8分
. 8分以
 为原点,与
为原点,与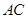 垂直的直线为
垂直的直线为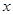 轴,
轴,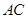 所在的直线为
所在的直线为 轴,
轴,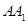 所在的直线为
所在的直线为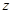 轴,建立空间直角坐标系
轴,建立空间直角坐标系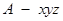 .
.
则
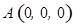 ,
,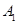
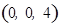 ,
,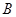
 ,
,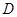
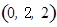 .
.∴
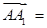
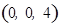 ,
,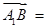
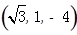 ,
,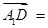
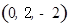 .设平面
.设平面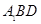 的法向量为
的法向量为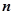
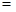
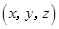 ,由
,由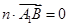 ,
,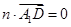 ,令
,令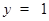 ,则
,则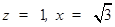 .
.∴平面
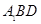 的一个法向量为
的一个法向量为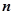
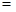
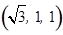 . 10分
. 10分∵
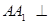 平面
平面 , ∴
, ∴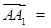
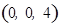 是平面
是平面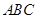 的一个法向量.
的一个法向量.∴
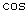
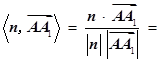
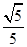 . 11分
. 11分∴平面
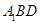 与平面
与平面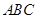 所成二面角(锐角)的余弦值为
所成二面角(锐角)的余弦值为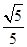 . 12分
. 12分点评:主要是考查了二面角的平面角的求解,以及线面平行的判定,属于基础题。

练习册系列答案
相关题目
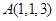 与点
与点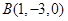 的距离为_____.
的距离为_____.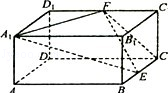
 中,已知
中,已知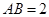 ,
,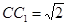 ,则异面直线
,则异面直线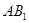 和
和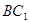 所成角的正弦值为( )
所成角的正弦值为( )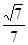
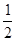
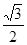
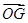 =x
=x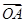 +y
+y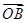 +z
+z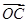 ,则(x,y,z)为( )
,则(x,y,z)为( ) 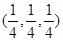
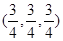
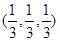
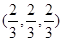
 与
与 平行,则
平行,则 = .
= . 中,
中,
 与
与 相交于
相交于 点.若
点.若 则
则 ( )
( )


