题目内容
【题目】椭圆![]() 中心在原点,焦点在
中心在原点,焦点在![]() 轴上,
轴上, ![]() 、
、![]() 分别为上、下焦点,椭圆的离心率为
分别为上、下焦点,椭圆的离心率为![]() ,
, ![]() 为椭圆上一点且
为椭圆上一点且![]() .
.
(1)若![]() 的面积为
的面积为![]() ,求椭圆
,求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 的延长线与椭圆
的延长线与椭圆![]() 另一交点为
另一交点为![]() ,以
,以![]() 为直径的圆过点
为直径的圆过点 ,
, ![]() 为椭圆上动点,求
为椭圆上动点,求![]() 的范围.
的范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据![]() 与椭圆的对称性可得
与椭圆的对称性可得![]() 为椭圆的左、右顶点,再由题设条件列出方程组,即可求出椭圆
为椭圆的左、右顶点,再由题设条件列出方程组,即可求出椭圆![]() 的方程;(2)由离心率得出
的方程;(2)由离心率得出![]() 之间的关系,由
之间的关系,由![]() 为直径的圆过点
为直径的圆过点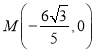 ,可得点
,可得点![]() 横坐标,再根据
横坐标,再根据![]() 三点共线,求出点
三点共线,求出点![]() 纵坐标,将点
纵坐标,将点![]() 坐标代入到椭圆方程化简可求出
坐标代入到椭圆方程化简可求出![]() 的值,即可得到椭圆方程,设点
的值,即可得到椭圆方程,设点![]() ,根据向量坐标表示出
,根据向量坐标表示出![]() ,根据
,根据![]() 取值范围即可求出
取值范围即可求出![]() 的范围.
的范围.
试题解析:(1)由椭圆的对称性可知, ![]() 为椭圆的左、右顶点,可设
为椭圆的左、右顶点,可设![]() ,
,
∴ 解得
解得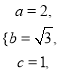 ∴
∴![]() .
.
(2)椭圆的离心率为![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
∵以![]() 为直径的圆过点
为直径的圆过点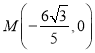 ,∴
,∴![]() .
.
又∵![]() 的延长线与椭圆
的延长线与椭圆![]() 另一交点为
另一交点为![]() ,则
,则![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
∴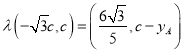 ,∴
,∴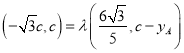 ,
,
∴![]() ,
, ![]() ,
,
又∵![]() 在椭圆中,则代入椭圆方程有
在椭圆中,则代入椭圆方程有![]() ,
, ![]() ,
, ![]() ,
,
设椭圆上动点![]() ,则
,则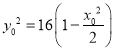 ,
, ![]() ,
,
∴![]()
![]() ,
, ![]() ,
,
∴![]() .
.

练习册系列答案
相关题目