Question

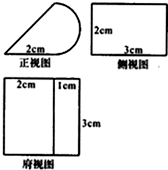某几何体的三视图如图，其正视图中的曲线部分为半个圆弧，则该几何体的体积为（　　）

• A．(2+

  3π

  2

  )cm³
• B．(6+

  3π

  2

  )cm³
• C．（2+3π）cm³
• D．（6+3π）cm³

Answer 1

分析：由三视图可知：该几何体是由左右两部分组成的，左边的是横放的直三棱柱，高为3，底面是边长为2的等腰直角三角形，右边是一个半圆柱，高为3，底面半径为1．据此即可计算出该几何体的体积．

解答：解：由三视图可知：该几何体是由左右两部分组成的，左边的是横放的直三棱柱，高为3，底面是边长为2的等腰直角三角形，右边是一个半圆柱，高为3，底面半径为1．
∴该几何体的体积V=

1

2

×2×2×3+

1

2

×π×12×3=（6+

3π

2

）（cm³）．
故选B．

点评：本题主要考查了由三视图求面积、体积，由三视图正确恢复原几何体是解题的关键．