Question

函数的性质通常指函数的定义域、值域、周期性、单调性、奇偶性等，请选择适当的探究顺序，研究函数f(x)=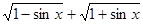的性质，并在此基础上，作出其在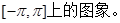

 

Answer 1

【答案】

解：① ∵∴的定义域为…………2分

② ∵

 ∴f(x)为偶函数；…………4分

③ ∵f(x+)=f(x),  ∴f(x)是周期为的周期函数；………6分

④ ∵

∴当时；

当时

（或当时f(x)=

∴当时单减；当时单增； 

又∵是周期为的偶函数   ∴f(x)的单调性为：

在上单增，在上单减。…………10分

⑤ ∵当时；

当时

∴的值域为：  …………12分

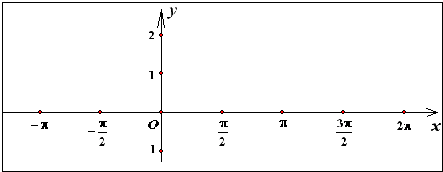
 ⑥由以上性质可得：在上的图象如上图所示：…………14分

【解析】本试题主要是考查了函数的性质的判定和求解的运用。

研究函数f(x)=的性质，根据先分析定义域和值域，奇偶性和单调性作出函数的图像，进而得到结论。