题目内容
已知圆的半径为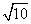 ,圆心在直线y=2x上,圆被直线x-y=0截得的弦长为4
,圆心在直线y=2x上,圆被直线x-y=0截得的弦长为4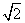 ,求圆的方程.
,求圆的方程.
解:方法一:设圆的方程是(x-a)2+(y-b)2=10.因为圆心在直线y=2x上,
所以b=2a. ①
解方程组 得2x2-2(a+b)x+a2+b2-10=0,
得2x2-2(a+b)x+a2+b2-10=0,
所以x1+x2=a+b,x1·x2= .由弦长公式得
.由弦长公式得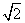 ·
· =4
=4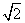 ,
,
化简得(a-b)2=4. ② 解①②组成的方程组,得a=2,b=4,
或a=-2,b=-4.故所求圆的方程是(x-2)2+(y-4)2=10,或(x+2)2+(y+4)2=10.
方法二:设圆的方程为(x-a)2+(y-b)2=10,则圆心为(a,b),半径r=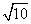 ,圆心(a,b)到直线x-y=0的距离d=
,圆心(a,b)到直线x-y=0的距离d=
由弦长、弦心距、半径组成的直角三角形得d2+( )2=r2,即
)2=r2,即 +8=10,
+8=10,
所以(a-b)2=4.又因为b=2a,所以a=2,b=4,或a=-2,b=-4.
故所求圆的方程是(x-2)2+(y-4)2=10,或(x+2)2+(y+4)2=10.

练习册系列答案
相关题目
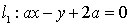 ,
,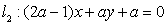 互相垂直,则
互相垂直,则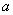 的值是( )
的值是( )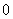 B.
B.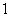 C.
C.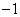
 ,则方程
,则方程 不能表示的曲线为
不能表示的曲线为 C.60° D.90°
C.60° D.90° 实数,若复数
实数,若复数 是纯虚数,则
是纯虚数,则 ( )
( ) B.
B. C.
C. D.
D. 
 的焦点为
的焦点为 是抛物线上横坐标不相等的两点,若
是抛物线上横坐标不相等的两点,若 的垂直平分线与
的垂直平分线与 轴的交点是
轴的交点是 ,则
,则 的最大值为 ( )
的最大值为 ( ) 的图象过定点
的图象过定点 B.
B. C.
C. D.
D.
