题目内容
设f(x)=cos2x+sinx,则下列结论正确的一个是( )
| A.f(x)的最大值为2,最小值为0 | ||
B.f(x)的最大值为
| ||
C.f(x)的最大值为
| ||
D.f(x)的最大值为
|
∵f(x)=cos2x+sinx=1-sin2x+sinx=-(sinx-
)2+
,
∵-1≤sinx≤1,
∴当sinx=
时,f(x)max=
,
当sinx=-1时,f(x)min=-1,
故选B.
| 1 |
| 2 |
| 5 |
| 4 |
∵-1≤sinx≤1,
∴当sinx=
| 1 |
| 2 |
| 5 |
| 4 |
当sinx=-1时,f(x)min=-1,
故选B.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 sinωxcosωx
sinωxcosωx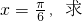 ω的值.
ω的值. sinωxcosωx
sinωxcosωx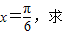 ω的值.
ω的值.