题目内容
若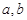 是两条异面直线,
是两条异面直线,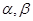 是两个不同平面,
是两个不同平面,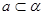 ,
,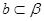 ,
,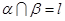 ,则
,则
A. 与 与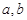 分别相交 分别相交 | B. 与 与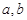 都不相交 都不相交 |
C. 至多与 至多与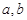 中一条相交 中一条相交 | D.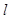 至少与 至少与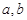 中的一条相交 中的一条相交 |
D
解析试题分析:如果 与
与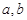 都不相交,则
都不相交,则 与
与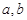 都平行,所以直线
都平行,所以直线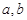 平行,与直线
平行,与直线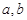 异面矛盾,所以
异面矛盾,所以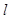 至少与
至少与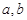 中的一条相交.
中的一条相交.
考点:本小题主要考查空间直线、平面的位置关系.
点评:判断空间直线、平面间的位置关系,要紧扣相应的判定定理和性质定理,发挥空间想象能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
设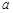 、
、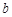 是不同的两条直线,
是不同的两条直线,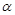 、
、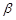 是不同的两个平面,分析下列命题,其中正确的是( ).
是不同的两个平面,分析下列命题,其中正确的是( ).
A.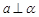 , ,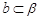 , ,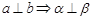 | B.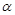 ∥ ∥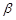 , ,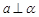 , ,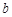 ∥ ∥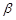 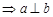 |
C.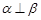 , ,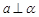 , ,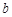 ∥ ∥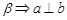 | D.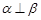 , ,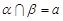 , , |
在三棱柱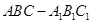 中,各侧面均为正方形,侧面
中,各侧面均为正方形,侧面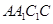 的对角线相交于点
的对角线相交于点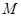 ,则
,则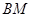 与平面
与平面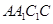 所成角的大小是( )
所成角的大小是( )
| A.30° | B.45° | C.60° | D.90 |
下列命题中假命题是
| A.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行 |
| B.垂直于同一条直线的两条直线相互垂直 |
| C.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 |
| D.若一个平面内的两条相交直线与另一个平面内的相交直线分别平行,那么这两个平面相互平行 |
如图,在正方体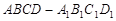 中,
中,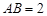 .则点
.则点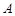 到面
到面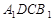 的距离是( )
的距离是( )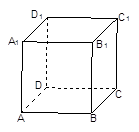
A.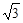 | B.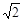 | C.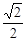 | D.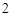 |
已知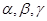 是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①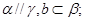 ②
②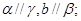 ③
③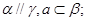 如果命题
如果命题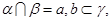 且_______,则
且_______,则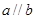 为真命题,则可以在横线处填入的条件是( )
为真命题,则可以在横线处填入的条件是( )
| A.①或② | B.②或③ | C.①或③ | D.只有② |
已知直线 a和平面?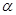 ,
,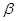 ,
,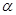 ∩
∩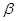 =l,a
=l,a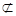
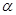 ,a
,a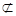
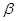 ,a在
,a在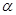 ,
,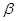 内的射影分别为直线 b 和 c ,则 b 和 c 的位置关系是( )
内的射影分别为直线 b 和 c ,则 b 和 c 的位置关系是( )
| A.相交或平行 | B.相交或异面 |
| C.平行或异面 | D.相交﹑平行或异面 |
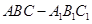 的侧棱与底面垂直,体积为
的侧棱与底面垂直,体积为 ,底面是边长为
,底面是边长为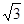 的正三角形,若
的正三角形,若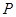 为底面
为底面 的中心,则
的中心,则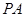 与平面
与平面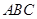 所成角的大小为( )
所成角的大小为( )