题目内容
如图,边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,将△AED,△EBF,△FCD分别沿DE,EF,FD折起,使A,B,C三点重合于点A′,若四面体A'EFD的四个顶点在同一个球面上,则该球的半径为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:把棱锥扩展为正四棱柱,求出正四棱柱的外接球的半径就是三棱锥的外接球的半径.
解答:解:由题意可知△A′EF是等腰直角三角形,且A′D⊥平面A′EF.
三棱锥的底面A′EF扩展为边长为1的正方形,
然后扩展为正四棱柱,三棱锥的外接球与正四棱柱的外接球是同一个球,
正四棱柱的对角线的长度就是外接球的直径,直径为:
=
.
∴球的半径为
.
故选:B.
三棱锥的底面A′EF扩展为边长为1的正方形,
然后扩展为正四棱柱,三棱锥的外接球与正四棱柱的外接球是同一个球,
正四棱柱的对角线的长度就是外接球的直径,直径为:
| 12+12+22 |
| 6 |
∴球的半径为
| ||
| 2 |
故选:B.
点评:本题考查几何体的折叠问题,几何体的外接球的半径的求法,考查空间想象能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
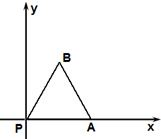 如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是
如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是 (2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是
(2011•洛阳一模)如图放置的边长为1的正三角形ABC沿x轴的正方向滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系是y=f(x).则f(x)在两个相邻零点间的图象与x轴围成的面积是 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.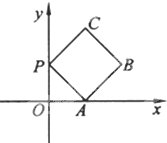 如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为
如图放置的边长为2的正方形PABC沿x轴滚动.设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),则f(x)的最小正周期为