题目内容
【题目】已知椭圆![]() :
:![]() ,过点
,过点![]() 且与
且与![]() 轴不重合的直线与
轴不重合的直线与![]() 相交于
相交于![]() 两点,点
两点,点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)当![]() 垂直于
垂直于![]() 轴时,求直线
轴时,求直线![]() 的方程;
的方程;
(2)证明:![]() .
.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)当![]() 垂直于
垂直于![]() 轴时,其方程为
轴时,其方程为![]() ,求出点
,求出点![]() 的坐标后可得直线
的坐标后可得直线![]() 的斜率,于是可得直线方程。(2)由于
的斜率,于是可得直线方程。(2)由于![]() 在
在![]() 轴上,所以只需证明点
轴上,所以只需证明点![]() 的纵坐标相等即可得到结论成立,解题时注意直线方程的设法.
的纵坐标相等即可得到结论成立,解题时注意直线方程的设法.
(1)设点![]() ,
,
当![]() 垂直于
垂直于![]() 轴时,可得
轴时,可得![]() ,所以
,所以![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,
,
又![]() ,
,
所以![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
(2)法一:
①当直线![]() 的斜率不存在时,其方程为
的斜率不存在时,其方程为![]() ,
,
若![]() ,则
,则![]() ,此时
,此时![]() 方程为
方程为![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,因此
,因此![]() ,所以
,所以![]() .
.
若![]() ,则
,则![]() ,此时
,此时![]() 方程为
方程为![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() ,因此
,因此![]() ,所以
,所以![]() .
.
综上可得![]() .
.
②当直线![]() 的斜率存在时,设
的斜率存在时,设![]() ,
,
由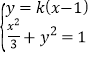 消去y整理得
消去y整理得![]() ,
,
其中![]() ,
,
设![]() ,
,![]() ,则
,则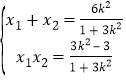 ,
,
因为![]() ,
,
所以直线![]() 的方程为
的方程为![]()
当![]() 时,得
时,得![]() ,
,
因为![]()
![]()
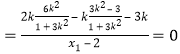 .
.
所以![]() ,
,
所以![]() .
.
法二:
设直线![]() ,
,
由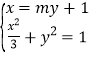 消去x整理得
消去x整理得![]() ,
,
其中![]() ,
,
设![]() ,
,![]() ,则
,则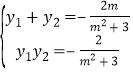 ,
,
所以![]() ,故
,故![]() 所以
所以![]() .
.
因为![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
当![]() 时,得
时,得![]() ,
,
所以![]() ,
,
所以![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】学生学习的自律性很重要.某学校对自律性与学生成绩是否有关进行了调研,从该校学生中随机抽取了100名学生,通过调查统计得到![]() 列联表的部分数据如下表:
列联表的部分数据如下表:
自律性一般 | 自律性强 | 合计 | |
成绩优秀 | 40 | ||
成绩一般 | 20 | ||
合计 | 50 | 100 |
(1)补全![]() 列联表中的数据;
列联表中的数据;
(2)判断是否有![]() 的把握认为学生的自律性与学生成绩有关.
的把握认为学生的自律性与学生成绩有关.
参考公式及数据: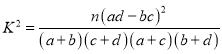 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |