题目内容
如图,椭圆
+
=1的两焦点F1,F2与短轴两端点B1,B2构成∠B2F1B1为120°,面积为2
的菱形.
(1)求椭圆的方程;
(2)若直线l:y=kx+m与椭圆相交于M,N两点(M,N不是左右顶点),且以MN为直径的圆过椭圆右顶点A,求证:直线l过定点,并求出该定点的坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(1)求椭圆的方程;
(2)若直线l:y=kx+m与椭圆相交于M,N两点(M,N不是左右顶点),且以MN为直径的圆过椭圆右顶点A,求证:直线l过定点,并求出该定点的坐标.
分析:(Ⅰ)由已知∠B2F1B1为=120°,及菱形F1B1F2B2的面积可得
,从而可求b,c,再由a=
可求,可求椭圆方程
(Ⅱ)设M(x1,y1),N(x2,y2),由
整理,结合方程的根与系数的关系可得,x1+x2=
,x1•x2=
,且△=64m2k2-16(3+4k2)(m2-3)>0,而以MN为直径的圆过椭圆的右顶点A可得
•
=0即x1x2+y1y2=0,代入可得m,k之间的关系,代入直线方程可知直线所过的定点
|
| b2+c2 |
(Ⅱ)设M(x1,y1),N(x2,y2),由
|
| -8mk |
| 3+4k2 |
| 4(m2-3) |
| 3+4k2 |
| AM |
| AN |
解答: 解:(Ⅰ)∵∠B2F1B1为=120°
解:(Ⅰ)∵∠B2F1B1为=120°
∴∠B1F1O=60°
tan60°=
=
∵菱形F1B1F2B2的面积S =2×
×2c×b=2
bc=
即
∴
,
由a=
=2
故椭圆方程为
+
=1.
(Ⅱ)设M(x1,y1),N(x2,y2),由
得(3+4k2)x2+8mkx+4(m2-3)=0,
则x1+x2=
,x1•x2=
,
且△=64m2k2-16(3+4k2)(m2-3)>0,即3+4k2-m2>0
∵以MN为直径的圆过椭圆的右顶点A
∴AM⊥AN即
•
=0
∴x1x2+y1y2=0,即y1y2+x1x2-2(x1+x2)+4=0,
又y1y2=(kx1+m)•(kx2+m)=k2x1x2+mk(x1+x2)+m2=
,
∴
+
+
+4=0,
化简得,7m2+4k2+16mk=0
解得m=-2k或m=-
且均满足3+4k2-m2>0
当m=-2k时,L:y=k(x-2),直线过定点(2,0)与已知矛盾;
当m=-
时,L;y=k(x-
),直线过定点(
,0)
综上,直线l过定点,定点坐标为(
,0)
 解:(Ⅰ)∵∠B2F1B1为=120°
解:(Ⅰ)∵∠B2F1B1为=120°∴∠B1F1O=60°
tan60°=
| b |
| c |
| 3 |
∵菱形F1B1F2B2的面积S =2×
| 1 |
| 2 |
| 3 |
bc=
| 3 |
即
|
∴
|
由a=
| b2+c2 |
故椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设M(x1,y1),N(x2,y2),由
|
则x1+x2=
| -8mk |
| 3+4k2 |
| 4(m2-3) |
| 3+4k2 |
且△=64m2k2-16(3+4k2)(m2-3)>0,即3+4k2-m2>0
∵以MN为直径的圆过椭圆的右顶点A
∴AM⊥AN即
| AM |
| AN |
∴x1x2+y1y2=0,即y1y2+x1x2-2(x1+x2)+4=0,
又y1y2=(kx1+m)•(kx2+m)=k2x1x2+mk(x1+x2)+m2=
| 3(m2-4k2) |
| 3+4k2 |
∴
| 3(m2-4k2) |
| 3+4k2 |
| 4(m2-3) |
| 3+4k2 |
| 16mk |
| 3+4k2 |
化简得,7m2+4k2+16mk=0
解得m=-2k或m=-
| 2k |
| 7 |
当m=-2k时,L:y=k(x-2),直线过定点(2,0)与已知矛盾;
当m=-
| 2k |
| 7 |
| 2 |
| 7 |
| 2 |
| 7 |
综上,直线l过定点,定点坐标为(
| 2 |
| 7 |
点评:本题主要考查了利用椭圆的性质求解椭圆的方程,直线与椭圆的相交关系的应用,方程的根与系数关系的应用,利用直线的点斜式求解直线所过的定点,属于直线与曲线的综合性试题

练习册系列答案
相关题目
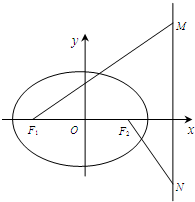 如图,椭圆
如图,椭圆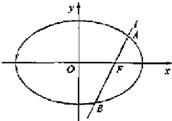 如图,椭圆
如图,椭圆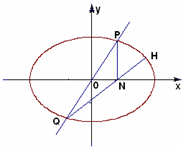 如图,椭圆
如图,椭圆 (2010•武清区一模)如图,椭圆
(2010•武清区一模)如图,椭圆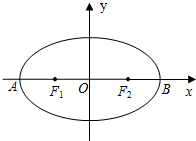 如图,椭圆
如图,椭圆