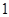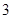题目内容
如图,已知 中,点
中,点 在线段
在线段 上, 点
上, 点 在线段
在线段 上且满足
上且满足 ,若
,若 ,则
,则 的值为
的值为
A. | B.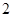 | C. | D. |
A
解析试题分析:根据题意,由于 中,点
中,点 在线段
在线段 上, 点
上, 点 在线段
在线段 上且满足
上且满足 ,
, ,那么结合已知条件中,由于
,那么结合已知条件中,由于 ,则可知
,则可知 ,结合已知的边和角可知,所求的数量积为-2,故选A.
,结合已知的边和角可知,所求的数量积为-2,故选A.
考点:向量的数量积的运用
点评:解决的冠军艾女士对于已知的三角形建立适当的坐标系,然后借助于向量的坐标法求解,或者运用向量的基本定理来变形得到,属于基础题。

练习册系列答案
相关题目
已知向量 ,
, ,若
,若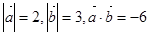 ,则
,则 的值为( )
的值为( )
A.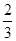 | B.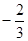 | C.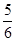 | D. |
在直角坐标系 中,
中, 分别是与
分别是与 轴,
轴, 轴平行的单位向量,若直角三角形
轴平行的单位向量,若直角三角形 中,
中, ,
, ,则
,则 的可能值有( )
的可能值有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
若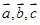 均为单位向量,且
均为单位向量,且 ,则
,则 的最大值为( )
的最大值为( )
| A.3 | B. | C.1 | D. +1 +1 |
设 R,向量
R,向量 ,且
,且 ,则
,则 ( )
( )
A.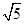 | B. | C. | D.10 |
在 所在的平面上有一点
所在的平面上有一点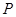 ,满足
,满足 ,则
,则 与
与 的面积之比是( )
的面积之比是( )
A. | B. | C. | D. |
已知平面上不共线的四点O,A,B,C,若 则
则 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
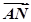 =λ
=λ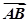 +μ
+μ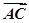 ,则λ+μ的值为 ( )
,则λ+μ的值为 ( )
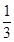

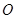 、
、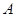 、
、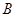 是平面上不共线的三点,向量
是平面上不共线的三点,向量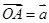 ,
,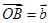 。设
。设 为线段
为线段 垂直平分线上任意一点,向量
垂直平分线上任意一点,向量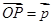 ,若
,若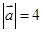 ,
,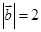 ,则
,则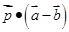 等于
等于