题目内容
在 所在的平面上有一点
所在的平面上有一点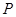 ,满足
,满足 ,则
,则 与
与 的面积之比是( )
的面积之比是( )
A. | B. | C. | D. |
D
解析试题分析: 由 , 得
, 得 ,
,
所以 , 即
, 即
所以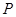 是
是 边上的第二个三等分点,故
边上的第二个三等分点,故 .
.
考点:平行向量
点评:本题考查的知识点是平行向量与共线向量,其中根据数乘向量的几何意义,分析出 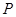 在
在 边上且为
边上且为 边上靠近
边上靠近 点的三等分点,是解答本题的关键.
点的三等分点,是解答本题的关键.

练习册系列答案
相关题目
如图,已知 中,点
中,点 在线段
在线段 上, 点
上, 点 在线段
在线段 上且满足
上且满足 ,若
,若 ,则
,则 的值为
的值为
A. | B. | C. | D. |
已知向量 ,则向量
,则向量 的夹角为 ( )
的夹角为 ( )
A. | B. | C. | D. |
已知 、
、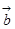 是非零向量且满足
是非零向量且满足 ,
, ,则向量
,则向量 与
与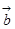 的
的
夹角是 ( )
A. | B. | C. | D. |
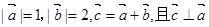 ,则向量
,则向量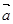 与
与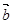 的夹角为( )
的夹角为( )
| A.30° | B.60° | C.120° | D.150° |
设向量 ,
, ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. | C. 与 与 垂直 垂直 | D. ∥ ∥ |
已知 ,O是坐标原点,则
,O是坐标原点,则 等于
等于
A. | B. | C. | D. |
 的最小值是( )
的最小值是( )




 =(cos
=(cos
 , sin
, sin ,
,  ,若△OAB是以O为直角顶点的等腰直角三角形,则△OAB的面积等于( )
,若△OAB是以O为直角顶点的等腰直角三角形,则△OAB的面积等于( )
