题目内容
已知函数f(x)=2x,x∈R.
(1)当m取何值时方程|f(x)-2|=m有一个解?两个解?
(2)若不等式f2(x)+f(x)-m>0在R上恒成立,求m的取值范围.
解:

(1)令F(x)=|f(x)-2|=|2x-2|,G(x)=m,画出F(x)的图象如图所示:
由图象看出,当m=0或m≥2时,函数F(x)与G(x)的图象只有一个交点,原方程有一个解;
当0<m<2时,函数F(x)与G(x)的图象有两个交点,原方程有两个解.
(2)令f(x)=t(t>0),H(t)=t2+t,
∵H(t)= -
- 在区间(0,+∞)上是增函数,
在区间(0,+∞)上是增函数,
∴H(t)>H(0)=0,因此要使t2+t>m在区间(0,+∞)上恒成立,应有m≤0,即所求m的取值范围为(-∞,0].

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
在一次数学实验中,运用计算器采集到如下一组数据:
| x | -2.0 | -1.0 | 0 | 1.0 | 2.0 | 3.0 |
| y | 0.24 | 0.51 | 1 | 2.02 | 3.98 | 8.02 |
则x、y的函数关系与下列哪类函数最接近(其中a、b为待定系数)( )
A.y=a+bx B.y=a+bx C.y=ax2+b D.y=a+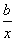
 则a、b、c的大小关系为( )
则a、b、c的大小关系为( )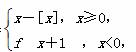 其中[x]表示不超过x的最大整数,如[-1.5]=-2,[1.5]=1,若直线y=k(x+1)(k>0)与函数y=f(x)的图象有三个不同的交点,则k的取值范围是( )
其中[x]表示不超过x的最大整数,如[-1.5]=-2,[1.5]=1,若直线y=k(x+1)(k>0)与函数y=f(x)的图象有三个不同的交点,则k的取值范围是( )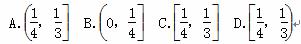
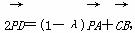 ,其中λ∈R,则P点一定在( )
,其中λ∈R,则P点一定在( )