题目内容
18.一个正三棱锥的三条侧棱长均为1,且两两垂直,将这个正三棱锥绕着它的高线旋转60°,则旋转后的三棱锥与原三棱锥公共部分的体积等于$\frac{\sqrt{2}}{18}$.分析 如图所示,PO为正三棱锥的高.旋转后的三棱锥与原三棱锥公共部分为正六棱锥P-DEFGHM.其中AO=$\frac{\sqrt{3}}{3}$,PO=$\sqrt{P{A}^{2}-A{O}^{2}}$,DE=$\frac{1}{3}$.即可得出.
解答 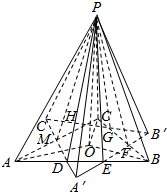 解:如图所示,PO为正三棱锥的高.
解:如图所示,PO为正三棱锥的高.
旋转后的三棱锥与原三棱锥公共部分为正六棱锥P-DEFGHM.
$AO=\frac{2}{3}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$.
PO=$\sqrt{P{A}^{2}-A{O}^{2}}$=$\frac{\sqrt{6}}{3}$.
DE=$\frac{1}{3}$.
∴要求的体积V=$\frac{1}{3}×PO×{S}_{正六边形DEFGHM}$
=$\frac{1}{3}×\frac{\sqrt{6}}{3}$×$6×\frac{\sqrt{3}}{4}×(\frac{1}{3})^{2}$
=$\frac{\sqrt{2}}{18}$.
故答案为:$\frac{\sqrt{2}}{18}$.
点评 本题考查了棱锥的体积计算公式、勾股定理、等边三角形的面积计算公式,考查了空间想象能力、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.设P=e0.3,Q=ln0.2,R=sin$\frac{15π}{7}$,则( )
| A. | P<R<Q | B. | R<Q<P | C. | R<P<Q | D. | Q<R<P |
6.根据下表,绘制网络图.
| 工作代码 | 紧前工作 | 紧后工作 | 工期/时 |
| A | C | G | 2 |
| B | D | 无 | 3 |
| C | 无 | A、D、F | 4 |
| D | C | B | 2 |
| E | F | 无 | 4 |
| F | C | E | 2 |
| G | A | 无 | 5 |
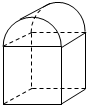 如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).
如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).