题目内容
 如图,在四棱锥D′-ABCE中,底面为直角梯形,AB=2BC=2CE=2,且AB⊥BC,AB∥CE,平面D′AE⊥平面ABCE.
如图,在四棱锥D′-ABCE中,底面为直角梯形,AB=2BC=2CE=2,且AB⊥BC,AB∥CE,平面D′AE⊥平面ABCE.(1)求证:AD′⊥EB;
(2)若D′A⊥D′E,D′A=D′E,求直线AC与平面ABD′所成角的正弦值.
分析:(1)取AB中点H,连接CH,则CH∥AE,由AB=2BC=2CE=2,可得四边形BCEH为正方形,从而可得BE⊥AE,进而可证BE⊥平面D′AE,故AD′⊥EB;
(2)D′在底面上的射影为AE中点G,设AC∩HE=0,过G作AB的垂线,垂足为F,连接D′F,过G作D′F的垂线,垂足为M,则GM等于O到面ABD′的距离,求出GM,AO的长,即可得到直线AC与平面ABD′所成角的正弦值.
(2)D′在底面上的射影为AE中点G,设AC∩HE=0,过G作AB的垂线,垂足为F,连接D′F,过G作D′F的垂线,垂足为M,则GM等于O到面ABD′的距离,求出GM,AO的长,即可得到直线AC与平面ABD′所成角的正弦值.
解答:(1)证明:∵平面D′AE⊥平面ABCE,
∴AD′在底面ABCE上的射影落在AE上
取AB中点H,连接CH,则CH∥AE
∵AB=2BC=2CE=2,∴四边形BCEH为正方形,
∴BE⊥CH,CH∥AE
∴BE⊥AE
∵平面D′AE⊥平面ABCE,平面D′AE∩平面ABCE=AE,
∴BE⊥平面D′AE
∴AD′⊥EB;
(2)解:由题意可知,D′在底面上的射影为AE中点G,设AC∩HE=0,则OG∥AB,∴G与O到平面ABD′的距离相等
过G作AB的垂线,垂足为F,连接D′F,过G作D′F的垂线,垂足为M,
则GM等于O到面ABD′的距离
在直角△D′GF中,FG=
,D′G-
,AO=
,∴GM=
设直线AC与平面ABD′所成角为α,则sinα=
=
∴直线AC与平面ABD′所成角的正弦值为
.
∴AD′在底面ABCE上的射影落在AE上
取AB中点H,连接CH,则CH∥AE
∵AB=2BC=2CE=2,∴四边形BCEH为正方形,
∴BE⊥CH,CH∥AE
∴BE⊥AE
∵平面D′AE⊥平面ABCE,平面D′AE∩平面ABCE=AE,
∴BE⊥平面D′AE
∴AD′⊥EB;

(2)解:由题意可知,D′在底面上的射影为AE中点G,设AC∩HE=0,则OG∥AB,∴G与O到平面ABD′的距离相等
过G作AB的垂线,垂足为F,连接D′F,过G作D′F的垂线,垂足为M,
则GM等于O到面ABD′的距离
在直角△D′GF中,FG=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 6 |
设直线AC与平面ABD′所成角为α,则sinα=
| ||||
|
| ||
| 15 |
∴直线AC与平面ABD′所成角的正弦值为
| ||
| 15 |
点评:本题考查线面垂直,考查线面角,解题的关键是掌握线面垂直的判定方法,求出点面距离,从而可求直线AC与平面ABD′所成角的正弦值,

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面为直角梯形,∠BAD=90°,BC∥AD且AD=2,AB=BC=1,PA=λ(λ>0).
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面为直角梯形,∠BAD=90°,BC∥AD且AD=2,AB=BC=1,PA=λ(λ>0). 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.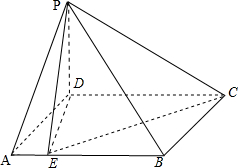 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC.已知
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC.已知