题目内容
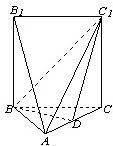 如图,五面体A-BCC1B1中,AB1=4.底面ABC是正三角形,AB=2.四边形BCC1B1是矩形,平面ABC⊥平面BCC1B1,D为AC的中点.
如图,五面体A-BCC1B1中,AB1=4.底面ABC是正三角形,AB=2.四边形BCC1B1是矩形,平面ABC⊥平面BCC1B1,D为AC的中点.(Ⅰ)证明AB1∥平面BDC1;
(Ⅱ)求三棱锥B1-ABC1的体积.
分析:(1)连接B1C交BC1于O,连接DO,根据四边形BCC1B1是矩形可判断出,O为B1C中点,进而利用D为AC中点,判断出DO∥AB1,进而根据线面平行的法则判断出AB1∥平面BDC1.
(2)首先根据勾股定理求得BB1,进而求得三角形BC1B1的面积,A到平面BCC1B1的距离为△ABC的高进而根据三棱锥的体积公式求得答案.
(2)首先根据勾股定理求得BB1,进而求得三角形BC1B1的面积,A到平面BCC1B1的距离为△ABC的高进而根据三棱锥的体积公式求得答案.
解答: 证明:(Ⅰ)连接B1C交BC1于O,连接DO,
证明:(Ⅰ)连接B1C交BC1于O,连接DO,
∵四边形BCC1B1是矩形
∴O为B1C中点
又D为AC中点,从而DO∥AB1
∵AB1?平面BDC1,DO?平面BDC1
∴AB1∥平面BDC1.
(Ⅱ)BB1=
=2
三角形BC1B1的面积S=
BB1×B1C1=
×2=2
A到平面BCC1B1的距离为△ABC的高
∴VB1-ABC1=VA-BC1B1=
×2
×
=2
因此,三棱锥B1-ABC1的体积为2.
 证明:(Ⅰ)连接B1C交BC1于O,连接DO,
证明:(Ⅰ)连接B1C交BC1于O,连接DO,∵四边形BCC1B1是矩形
∴O为B1C中点
又D为AC中点,从而DO∥AB1
∵AB1?平面BDC1,DO?平面BDC1
∴AB1∥平面BDC1.
(Ⅱ)BB1=
| AB12-AB2 |
| 3 |
三角形BC1B1的面积S=
| 1 |
| 2 |
2
| ||
| 2 |
| 3 |
A到平面BCC1B1的距离为△ABC的高
| 3 |
∴VB1-ABC1=VA-BC1B1=
| 1 |
| 3 |
| 3 |
| 3 |
因此,三棱锥B1-ABC1的体积为2.
点评:本题主要考查了直线与平面平行的判定和三棱锥体积的计算.考查了学生对所学知识的理解和灵活利用.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
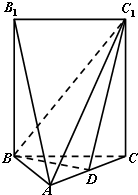 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.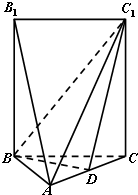 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角. 如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.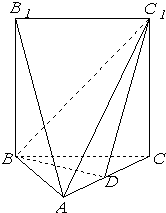 如图,五面体A-BCC1B1中,AB1=4,底面ABC是正三角形,AB=2,四边形BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图,五面体A-BCC1B1中,AB1=4,底面ABC是正三角形,AB=2,四边形BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.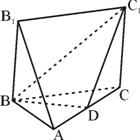 (1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;
(1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;