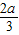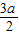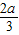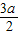题目内容

若sin（180°+α）=-
10
10
，0°＜α＜90°．求
sin(-α)+sin(-90°-α)
cos(540°-α)+cos(-270°-α)
的值．
分析：依题意，可求得sin α=
10
10
，cos α=
3
10
10
，对所求关系式先化简，再将cosα、sinα的值代入计算即可．
解答：解：由sin（180°+α）=-
10
10
，α∈（0°，90°），
得sin α=
10
10
，cos α=
3
10
10
，
∴原式=
-sinα-sin(90°+α)
cos(360°+180°-α)+cos(270°+α)

=
-sinα-cosα
-cosα+sinα

=
-
10
10
-
3
10
10
-
3
10
10
+
10
10

=2．
点评：本题考查运用诱导公式化简求值，考查运算能力，属于中档题．
练习册系列答案
相关题目
若sin（180°+α）+cos（90°+α）=-a，则cos（270°-α）+2sin（360°-α）的值是（　　）
若sin（180°+α）+cos（90°+α）=m，则cos（270°-α）+2sin（360°-α）的值为（　　）
若sin（180°+α）=-
10
10
，0°＜α＜90°．求
sin(-α)+sin(-90°-α)
cos(540°-α)+cos(-270°-α)
的值．
若sin（180°+α）+cos（90°+α）=-a，则cos（270°-α）+2sin（360°-α）的值是（ ）
A．-
B．-
C．
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网