题目内容
若sin（180°+α）+cos（90°+α）=-a，则cos（270°-α）+2sin（360°-α）的值是（ ）A．-
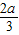
B．-
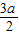
C．
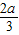
D．
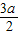
【答案】分析：利用诱导公式可求得sinα=
，继而可求得cos（270°-α）+2sin（360°-α）的值．
解答：解：∵sin（180°+α）+cos（90°+α）=-sinα-sinα=-a，
∴sinα=
．
∴cos（270°-α）+2sin（360°-α）
=cos（180°+90°-α）+2sin（360°-α）
=-cos（90°-α）-2sinα
=-sinα-2sinα
=-3sinα=-3×
=-
a．
故选B．
点评：本题考查三角函数的诱导公式，求得sinα=
是关键，属于基础题．
，继而可求得cos（270°-α）+2sin（360°-α）的值．解答：解：∵sin（180°+α）+cos（90°+α）=-sinα-sinα=-a，
∴sinα=
．∴cos（270°-α）+2sin（360°-α）
=cos（180°+90°-α）+2sin（360°-α）
=-cos（90°-α）-2sinα
=-sinα-2sinα
=-3sinα=-3×
=-a．故选B．
点评：本题考查三角函数的诱导公式，求得sinα=
是关键，属于基础题． 
练习册系列答案
相关题目
B.-
C.
D.
