题目内容
已知椭圆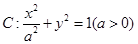 的右顶点为
的右顶点为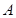 ,上顶点为
,上顶点为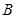 ,直线
,直线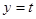 与椭圆交于不同的两点
与椭圆交于不同的两点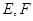 ,若
,若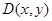 是以
是以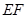 为直径的圆上的点,当
为直径的圆上的点,当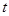 变化时,
变化时,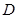 点的纵坐标
点的纵坐标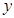 的最大值为
的最大值为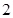 .
.
(Ⅰ)求椭圆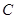 的方程;
的方程;
(Ⅱ)过点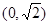 且斜率
且斜率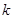 为的直线
为的直线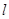 与椭圆
与椭圆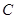 交于不同的两点
交于不同的两点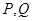 ,是否存在
,是否存在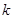 ,使得向量
,使得向量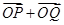 与
与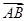 共线?若存在,试求出
共线?若存在,试求出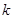 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
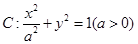 的右顶点为
的右顶点为 ,上顶点为
,上顶点为 ,直线
,直线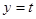 与椭圆交于不同的两点
与椭圆交于不同的两点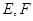 ,若
,若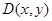 是以
是以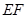 为直径的圆上的点,当
为直径的圆上的点,当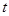 变化时,
变化时,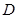 点的纵坐标
点的纵坐标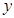 的最大值为
的最大值为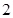 .
.(Ⅰ)求椭圆
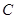 的方程;
的方程;(Ⅱ)过点
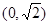 且斜率
且斜率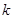 为的直线
为的直线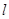 与椭圆
与椭圆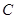 交于不同的两点
交于不同的两点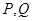 ,是否存在
,是否存在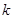 ,使得向量
,使得向量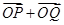 与
与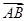 共线?若存在,试求出
共线?若存在,试求出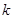 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.20.解:(1)由
 ,
,
 ,圆心为
,圆心为
以EF为直径的圆的方程为: 2分
2分
 (当
(当 时取等)
时取等)
令 则
则
依题
椭圆C的方程为: 6分
6分
(2) ,由
,由 消去y:
消去y:

设 ,PQ的中点M
,PQ的中点M
由点差法:
即 ①
①
M在直线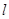 上
上 ②
②
又

 ,而
,而 与
与 共线,可得
共线,可得 //
//
 ③,
③,
由①②③得 , 12分
, 12分
这与 矛盾,故不存在 13分
矛盾,故不存在 13分

 ,
,
 ,圆心为
,圆心为
以EF为直径的圆的方程为:
 2分
2分 (当
(当 时取等)
时取等)令
 则
则
依题

椭圆C的方程为:
 6分
6分(2)
 ,由
,由 消去y:
消去y:

设
 ,PQ的中点M
,PQ的中点M
由点差法:

即
 ①
①M在直线
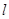 上
上 ②
②又


 ,而
,而 与
与 共线,可得
共线,可得 //
//
 ③,
③,由①②③得
 , 12分
, 12分这与
 矛盾,故不存在 13分
矛盾,故不存在 13分略

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 的左右焦点是F1,F2,设P是双曲线右支上一点,
的左右焦点是F1,F2,设P是双曲线右支上一点, 在
在 上的投影的大小恰好为|
上的投影的大小恰好为| ,则双曲线的离心率e为
,则双曲线的离心率e为



 的共同焦点为
的共同焦点为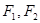 ,
,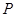 是两曲线的一个交点,则
是两曲线的一个交点,则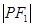 ·
· 的值为______________.
的值为______________. =1的右焦点重合,该抛物线上有一点M,它在y轴上的射影为N,则|MA|+|MN|的最小值为___________。
=1的右焦点重合,该抛物线上有一点M,它在y轴上的射影为N,则|MA|+|MN|的最小值为___________。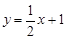 过椭圆
过椭圆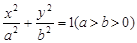 的一个焦点和一个顶点,则椭圆的离心率为( )
的一个焦点和一个顶点,则椭圆的离心率为( )
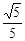
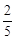
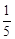
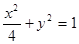 的长轴长等于 ▲ .
的长轴长等于 ▲ .
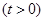 在直线
在直线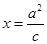 (
(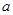 为长半轴,
为长半轴,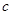 为半焦距)上.
为半焦距)上.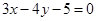 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;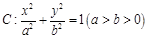 的离心率为
的离心率为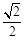 ,其中左焦点
,其中左焦点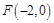
 的方程
的方程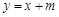 与椭圆
与椭圆 ,且线段
,且线段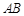 的中
的中 点
点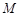 关于直线
关于直线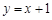 的对称点在圆
的对称点在圆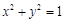 上,求
上,求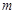 的值
的值 的离心率为
的离心率为 ,则
,则 的值为_____________.
的值为_____________.