题目内容
已知![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ;数列
;数列![]() 满足:
满足:![]() ,
,
![]() ,其前
,其前![]() 项和为
项和为![]()
⑴求数列![]() 、
、![]() 的通项公式;
的通项公式;
⑵设![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ,求使不等式
,求使不等式![]() 对
对![]() 都成立的最大正整数
都成立的最大正整数![]() 的值.
的值.
⑴![]()
![]() ⑵最大正整数
⑵最大正整数![]() 的值为
的值为![]()
解析:
⑴利用![]() 与
与![]() 的关系式及等差数列的通项公式可求;⑵求出
的关系式及等差数列的通项公式可求;⑵求出![]() 后,判断
后,判断![]() 的单调性.⑴
的单调性.⑴![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,![]()
![]() ;
;
![]()
![]() ,
,![]()
![]() 是等差数列,设其公差为
是等差数列,设其公差为![]() .
.
则 ,
,
![]()
![]() .
.
⑵![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() 是单调递增数列.
是单调递增数列.
![]() 当
当![]() 时,
时,![]()
![]()
![]() 对
对![]() 都成立
都成立![]()
![]() 所求最大正整数
所求最大正整数![]() 的值为
的值为![]() .
.
【名师指引】本题综合考察等差数列、通项求法、数列求和、不等式等知识,利用了函数、方程思想,这是历年高考的重点内容.

练习册系列答案
相关题目
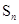 为数列
为数列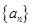 的前
的前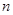 项和,且
项和,且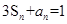 ,数列
,数列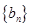 满足
满足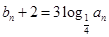 ,数列
,数列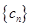 满足
满足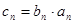 .
. .
.