题目内容
已知定义域为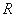 的函数
的函数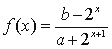 是奇函数.
是奇函数.
(Ⅰ)求a,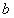 的值;
的值;
(Ⅱ)判断函数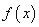 的单调性,并用函数的单调性定义证明;
的单调性,并用函数的单调性定义证明;
(Ⅲ)若对于任意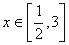 都有
都有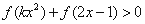 成立,求实数
成立,求实数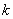 的取值范围.
的取值范围.
解:(Ⅰ)因为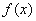 在定义域为
在定义域为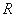 上是奇函数,所以
上是奇函数,所以 =0,
=0,
即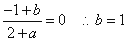
又由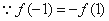 ,即
,即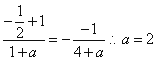
(Ⅱ)由(1)知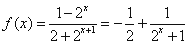 ,
,
任取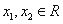 ,设
,设
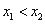 则
则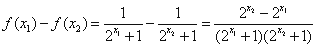
因为函数y=2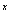 在R上是增函数且
在R上是增函数且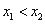 ∴
∴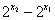 >0
>0
又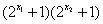 >0 ∴
>0 ∴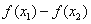 >0即
>0即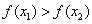
∴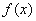 在
在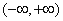 上为减函数.
上为减函数.
(Ⅲ)因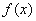 是奇函数,从而不等式:
是奇函数,从而不等式: 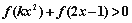
等价于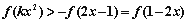 ,
,
因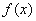 为减函数,由上式推得:
为减函数,由上式推得: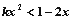 .
.
即对一切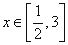 有:
有: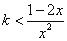 恒成立, ..
恒成立, ..
设 ,令
,令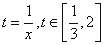 ,
,
则有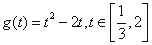 ,
,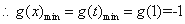
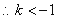 ,即k的取值范围为
,即k的取值范围为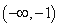 。
。

练习册系列答案
相关题目
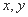 满足
满足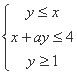 ,若
,若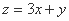 的最大值为
的最大值为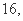 则
则
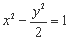 ,过定点P(2,1)作直线l交双曲线于P1、P2两点,并使得点P为线段P1P2的中点,则此直线l的方程为 ;
,过定点P(2,1)作直线l交双曲线于P1、P2两点,并使得点P为线段P1P2的中点,则此直线l的方程为 ;
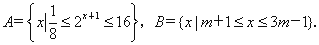
 中,
中, ,
, 分别是
分别是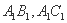 的中点,若
的中点,若 ,则
,则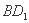 与
与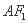 所成角的正切值 ( )
所成角的正切值 ( )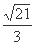 B、
B、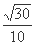 C、
C、 D、
D、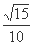
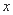 轴上,左右焦点分别为
轴上,左右焦点分别为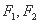 ,且它们在第一象限的交点为
,且它们在第一象限的交点为 ,
,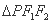 是以
是以 为底边的等腰三角形。若
为底边的等腰三角形。若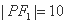 ,双曲线的离心率的取值范围为
,双曲线的离心率的取值范围为 ,则该椭圆的离心率
,则该椭圆的离心率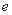 的取值范围是_______;
的取值范围是_______; 中,
中,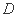 是棱
是棱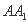 的中点,平面
的中点,平面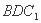 分此棱柱为上下两部分,则这上下两部分体积的比为
分此棱柱为上下两部分,则这上下两部分体积的比为 (B)
(B)
 (D)
(D)

 存在与直线
存在与直线 平行的切线,则实数
平行的切线,则实数 的取值范围是 .
的取值范围是 .