题目内容

$数学公式$ =________．

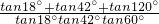-1
分析：根据60°=18°+42°，由两角和的正切函数公式化简后，得到tan18°+tan42°与tan18°tan42°的关系，然后把所求的式子利用特殊角的三角函数值化简后，将得到的关系式代入，化简后即可求出值．
解答：由tan60°=tan（18°+42°）= $\text{[math]}$ = $\text{[math]}$ ，
得到tan18°+tan42°= $\text{[math]}$ - $\text{[math]}$ tan18°tan42°，
则 $\text{[math]}$
= $\text{[math]}$
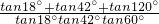
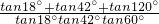
= $\text{[math]}$ =-1．
故答案为：-1
点评：此题考查学生灵活运用两角和的正切函数公式化简求值，是一道基础题．学生做题时注意角度的变换．

练习册系列答案

一天一练系列答案

一线调研今年新试卷系列答案

金版课堂课时训练系列答案

单元全能练考卷系列答案

小学同步全程测试卷一考通系列答案

新黄冈兵法密卷系列答案

特优练考卷系列答案

一通百通顶尖单元练系列答案

快乐AB卷系列答案

轻松赢考期末卷系列答案

相关题目

（本题满分8分．老教材试题第1小题4分，第2小题4分；新教材试题第1小题3分，第2小题5分．）
（老教材）
设a为实数，方程2x²-8x+a+1=0的一个虚根的模是 $数学公式$ ．
（1）求a的值；
（2）在复数范围内求方程的解．（新教材）
设函数f（x）=2^x+p，（p为常数且p∈R）
（1）若f（3）=5，求f（x）的解析式；
（2）在满足（1）的条件下，解方程：f^-1（x）=2+log₂x²．

下列说法中错误的是

A.
如果变量x与y之间存在着线性相关关系，则我们根据试验数据得到的点（x_i，y_i）（i=1，2，…，n）将散布在某一条直线的附近
B.
如果两个变量x与y之间不存在着线性关系，那么根据它们的一组数据（x_i，y_i）（i=1，2，…，n）不能写出一个线性方程
C.
设x，y是具有相关关系的两个变量，且x关于y的线性回归方程为 $数学公式$ =bx+a，b叫做回归系数
D.
为使求出的线性回归方程有意义，可用统计检验的方法来判断变量y与x之间是否存在线性相关关系

【待处理】已知|a|=10，|b|=12，且（3a）•（ $数学公式$ b）=-36，则a与b的夹角是

A.
60°
B.
120°
C.
135°
D.
150°

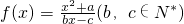对于函数f（x），若存在x₀∈R，使得f（x₀）=x₀，则称x₀为函数f（x）的不动点，若函数 $数学公式$ 有且仅有两个不动点0和2，且 $数学公式$ ．
（1）试求函数f（x）的表达式；
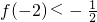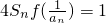（2）已知各项不为0的数列{a_n}满足 $数学公式$ ，其中S_n表示数列{a_n}的前n项和，求数列{a_n}的通项公式．

四面体ABCD四个面的重心分别为E、F、G、H，则四面体EFGH的表面积与四面体ABCD的表面积的比值是

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

如图，在平面直角坐标系xOy中，椭圆 $数学公式$ + $数学公式$ =1（a＞b＞0）被围于由4条直线x=±a，y=±b所围成的矩形ABCD内，任取椭圆上一点P，若 $数学公式$ =m• $数学公式$ +n• $数学公式$ （m、n∈R），则m、n满足的一个等式是________．

已知m＞1，且存在x∈[-2，0]，使不等式x²+2mx+m²-m≤0成立，则m的最大值为________．

函数y=f（x）定义在区间（-3，7）上，其导函数如右图所示，则函数y=f（x）在区间（-3，7）上极小值的个数是________个．