题目内容
对于函数f(x),若存在x0∈R,使得f(x0)=x0,则称x0为函数f(x)的不动点,若函数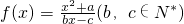 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且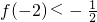 .
.
(1)试求函数f(x)的表达式;
(2)已知各项不为0的数列{an}满足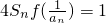 ,其中Sn表示数列{an}的前n项和,求数列{an}的通项公式.
,其中Sn表示数列{an}的前n项和,求数列{an}的通项公式.
解:(1)设 =x?(1-b)x2+cx+a=0有两个不等实根0和2
=x?(1-b)x2+cx+a=0有两个不等实根0和2
?a=0且2b-c=2且b≠1
?f(x)= .
.
由f(-2)<- ?-1<c<3
?-1<c<3
?c=2,b=2?f(x)= (x≠1).
(x≠1).
(2)由已知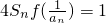 ,
,
可得2Sn=an-an2,
当n≥2时,2Sn-1=an-1-an-12,
两式相减得an=-an-1,或an-an-1=-1.
当n=1时,a1=-1,
由an=-an-1?a2=1不在定义域范围内应舍去,
故an-an-1=-1?an=-n.
分析:(1)利用函数f(x)=x的不动点,推出a,b,c的关系,通过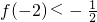 ,结合b,c∈N*,求出b,c,得到函数的表达式;
,结合b,c∈N*,求出b,c,得到函数的表达式;
(2)通过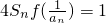 ,推出2Sn=an-an2,通过Sn-Sn-1=an,求数列{an}的通项公式.
,推出2Sn=an-an2,通过Sn-Sn-1=an,求数列{an}的通项公式.
点评:本题是中档题,考查数列与函数的综合问题,数列通项公式的求法,函数的基本性质的应用,考查逻辑推理能力,计算能力.
 =x?(1-b)x2+cx+a=0有两个不等实根0和2
=x?(1-b)x2+cx+a=0有两个不等实根0和2?a=0且2b-c=2且b≠1
?f(x)=
 .
.由f(-2)<-
 ?-1<c<3
?-1<c<3?c=2,b=2?f(x)=
 (x≠1).
(x≠1).(2)由已知
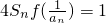 ,
,可得2Sn=an-an2,
当n≥2时,2Sn-1=an-1-an-12,
两式相减得an=-an-1,或an-an-1=-1.
当n=1时,a1=-1,
由an=-an-1?a2=1不在定义域范围内应舍去,
故an-an-1=-1?an=-n.
分析:(1)利用函数f(x)=x的不动点,推出a,b,c的关系,通过
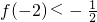 ,结合b,c∈N*,求出b,c,得到函数的表达式;
,结合b,c∈N*,求出b,c,得到函数的表达式;(2)通过
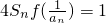 ,推出2Sn=an-an2,通过Sn-Sn-1=an,求数列{an}的通项公式.
,推出2Sn=an-an2,通过Sn-Sn-1=an,求数列{an}的通项公式.点评:本题是中档题,考查数列与函数的综合问题,数列通项公式的求法,函数的基本性质的应用,考查逻辑推理能力,计算能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目