题目内容
18.若25a=53b=102c.试求a、b、c之间的关系.分析 化指数式为对数式,然后利用对数的运算性质得答案.
解答 解:设25a=53b=102c=k,
则a=$\frac{1}{5}$log2k,b=$\frac{1}{3}$log5k,c=$\frac{1}{2}$lgk,
∴logk2=$\frac{1}{5a}$,logk5=$\frac{1}{3b}$,$lo{g}_{\frac{1}{2}}10=\frac{1}{2c}$,
又logk2+logk5=logk10,
∴$\frac{1}{5a}+\frac{1}{3b}=\frac{1}{2c}$.
点评 本题考查对数的运算性质,考查了指数式和对数式的互化,是基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
13.已知三个点A(0,1),B(1,3),c(2,a)在一条直线上,则a=( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
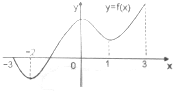 如图是定义在区间[-3,3]上的函数y=f(x)的图象,研究下列问题:
如图是定义在区间[-3,3]上的函数y=f(x)的图象,研究下列问题: