题目内容
6.正四棱锥的顶点都在同一球面上,若该棱锥的高为2,底面边长为2,则该球的表面积为9π.分析 正四棱锥P-ABCD的外接球的球心在它的高PE上,求出球的半径,求出球的表面积.
解答 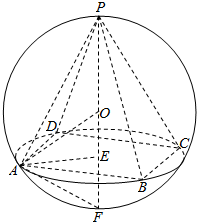 解:如图,正四棱锥P-ABCD中,PE为正四棱锥的高,根据球的相关知识可知,正四棱锥的外接球的球心O必在正四棱锥的高线PE所在的直线上,延长PE交球面于一点F,连接AE,AF,由球的性质可知△PAF为直角三角形且AE⊥PF,根据平面几何中的射影定理可得PA2=PF•PE,因为AE=$\sqrt{2}$,
解:如图,正四棱锥P-ABCD中,PE为正四棱锥的高,根据球的相关知识可知,正四棱锥的外接球的球心O必在正四棱锥的高线PE所在的直线上,延长PE交球面于一点F,连接AE,AF,由球的性质可知△PAF为直角三角形且AE⊥PF,根据平面几何中的射影定理可得PA2=PF•PE,因为AE=$\sqrt{2}$,
所以侧棱长PA=$\sqrt{4+2}$=$\sqrt{6}$,PF=2R,
所以6=2R×2,所以R=$\frac{3}{2}$,
所以S=4πR2=9π.
故答案为:9π.
点评 本题考查球的表面积,球的内接几何体问题,考查计算能力,是基础题.

练习册系列答案
相关题目
14.已知函数f(x)=x|x|,若对任意的x≤1有f(x+m)+f(x)<0恒成立,则实数m的取值范围是( )
| A. | (-∞,-1) | B. | (-∞,-1] | C. | (-∞,-2) | D. | (-∞,-2] |
1.函数f(x)=$\frac{lg(x+2)}{x-1}$的定义域是( )
| A. | (-2,1) | B. | [-2,1)∪(1,+∞) | C. | (-2,+∞) | D. | (-2,1)∪(1,+∞) |
18.甲乙两人下棋,甲获胜的概率为30%,甲不输的概率为80%,则甲乙下成和棋的概率为( )
| A. | 70% | B. | 30% | C. | 20% | D. | 50% |
16.i是虚数单位,复数2i=z(-1+i),则z的共轭复数是( )
| A. | -1+i | B. | -i+1 | C. | i+1 | D. | -i-1 |
