题目内容
已知 ,点
,点 依次满足
依次满足 。
。
(1)求点 的轨迹;
的轨迹;
(2)过点 作直线
作直线 交以
交以 为焦点的椭圆于
为焦点的椭圆于 两点,线段
两点,线段 的中点到
的中点到 轴的距离为
轴的距离为 ,且直线
,且直线 与点
与点 的轨迹相切,求该椭圆的方程;
的轨迹相切,求该椭圆的方程;
(3)在(2)的条件下,设点 的坐标为
的坐标为 ,是否存在椭圆上的点
,是否存在椭圆上的点 及以
及以 为圆心的一个圆,使得该圆与直线
为圆心的一个圆,使得该圆与直线 都相切,如存在,求出
都相切,如存在,求出 点坐标及圆的方程,如不存在,请说明理由.
点坐标及圆的方程,如不存在,请说明理由.
(1) 以原点为圆心,1为半径的圆, (2) 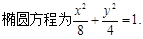 (3)存在点
(3)存在点 ,其坐标为
,其坐标为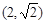 或
或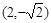 .
.
解析试题分析:(1)求动点轨迹方程,分四步.第一步,设动点坐标 第二步建立等量关系:
第二步建立等量关系: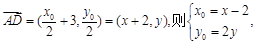 第三步化简等量关系:
第三步化简等量关系: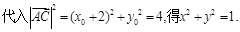 第四步,去杂.求轨迹,不仅求出轨迹方程,而且说明轨迹形状.(2)求椭圆标准方程,一般利用待定系数法. 设直线
第四步,去杂.求轨迹,不仅求出轨迹方程,而且说明轨迹形状.(2)求椭圆标准方程,一般利用待定系数法. 设直线 的方程为
的方程为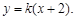 椭圆的方程
椭圆的方程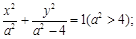 由
由 与圆相切得:
与圆相切得: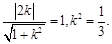 由直线
由直线 的方程与椭圆方程联立方程组得:
的方程与椭圆方程联立方程组得: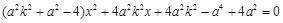 所以
所以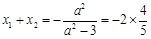 ,
,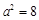 ∴
∴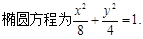 (3)存在性问题,一般从假设存在出发,列等量关系,将存在性问题转化为方程是否有解问题. 假设
(3)存在性问题,一般从假设存在出发,列等量关系,将存在性问题转化为方程是否有解问题. 假设 ,
, :
: 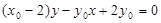
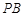 :
:  ,
,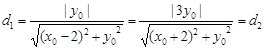
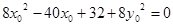
又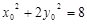 ,解得:
,解得: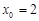 或
或 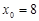 (舍).
(舍).
解析:(1) 设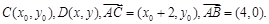
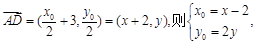
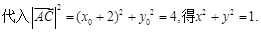
所以,点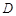 的轨迹是以原点为圆心,1为半径的圆. 4分
的轨迹是以原点为圆心,1为半径的圆. 4分
(2)设直线 的方程为
的方程为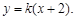 ①
①
椭圆的方程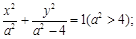 ②
②
由 与圆相切得:
与圆相切得: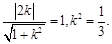 6分
6分
将①代入②得: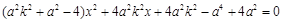 ,
,
又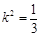 ,可得
,可得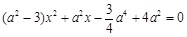 ,
,
有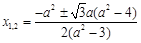 ,∴
,∴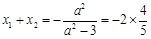 ,
,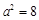 .
.
∴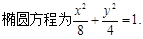 9分
9分
(3) 假设存在椭圆上的一点 ,使得直线
,使得直线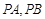 与以Q为圆心的圆相切,
与以Q为圆心的圆相切,
则Q到直线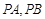 的距离相等,
的距离相等, 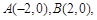
 :
: 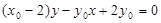
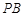 :
: 
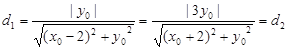 12分
12分
化简整理得: 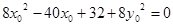
∵ 点在椭圆上,∴ 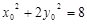
解得: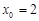 或
或 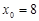 (舍)
(舍)  时,
时,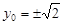 ,
,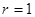 , &n
, &n

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
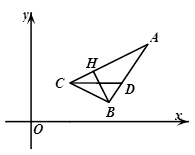
 的三个顶点是
的三个顶点是 求
求 边上的高所在直线的方程;
边上的高所在直线的方程;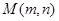 为圆C上任意一点,求
为圆C上任意一点,求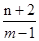 的最大值与最小值;
的最大值与最小值;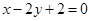 垂直,且在两坐标轴上截距之和为3的直线
垂直,且在两坐标轴上截距之和为3的直线 的方程?
的方程? 的方程为
的方程为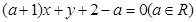 .
. 的取值范围。
的取值范围。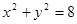 内有一点
内有一点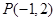 ,
,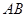 为过点
为过点 且倾斜角为
且倾斜角为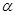 的弦,
的弦,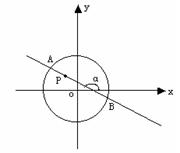
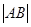 ;
;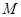 ,求点
,求点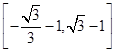 ,求直线AB的倾斜角α的取值范围.
,求直线AB的倾斜角α的取值范围.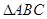 的顶点
的顶点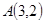 ,
,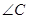 的平分线
的平分线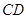 所在直线方程为
所在直线方程为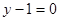 ,
,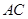 边上的高
边上的高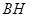 所在直线方程为
所在直线方程为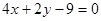 .
.
 的坐标;
的坐标;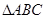 的面积.
的面积.  ,则实数
,则实数 的值为_____________.
的值为_____________.