题目内容
设f(x)=4cos2x•cos(2x+
)-1．
（1）当x∈[-
，
]时，求f（x）的值域；
（2）把f（x）的图象向右平移m（m＞0）个单位后所得图象关于y轴对称，求m的最小值．
| π |
| 3 |
（1）当x∈[-
| π |
| 48 |
| π |
| 4 |
（2）把f（x）的图象向右平移m（m＞0）个单位后所得图象关于y轴对称，求m的最小值．
分析：（1）利用三角函数的恒等变换化简f（x）的解析式为2cos（4x+
），通过x的范围求出相位的范围，由此求得f（x）的值域．
（2）先求出平移后函数due解析式，根据图象关于直线x=0对称，故有-4m+
=kπ，k∈Z，由此求得正数m的最小值．
| π |
| 3 |
（2）先求出平移后函数due解析式，根据图象关于直线x=0对称，故有-4m+
| π |
| 3 |
解答：解：（1）∵f（x）=4cos2x•（
cos2x-
sin2x）-1=2cos22x-2
sin2x•cos2x-1
=cos4x-
sin4x=2cos（4x+
），（4分）
因为x∈[-
，
]
∴4x+
∈[
，
]，
f（x）的最小值为-2，函数的最大值为：1．（6分）
∴f（x）的值域：[-2，1]．（7分）
（2）f（x）图象向右平移m个单位后所得图象对应的解析式为
y=2cos[4（x-m）+
]=2cos（4x-4m+
），（9分）
其为偶函数，那么图象关于直线x=0对称，故有：-4m+
=kπ，k∈Z
∴m=
-
所以正数m的最小值为
．（12分）．
| 1 |
| 2 |
| ||
| 2 |
| 3 |
=cos4x-
| 3 |
| π |
| 3 |
因为x∈[-
| π |
| 48 |
| π |
| 4 |
∴4x+
| π |
| 3 |
| π |
| 4 |
| 4π |
| 3 |
f（x）的最小值为-2，函数的最大值为：1．（6分）
∴f（x）的值域：[-2，1]．（7分）
（2）f（x）图象向右平移m个单位后所得图象对应的解析式为
y=2cos[4（x-m）+
| π |
| 3 |
| π |
| 3 |
其为偶函数，那么图象关于直线x=0对称，故有：-4m+
| π |
| 3 |
∴m=
| π |
| 12 |
| kπ |
| 4 |
| π |
| 12 |
点评：本题主要考查三角函数的恒等变换及化简求值，函数y=Asin（ωx+∅）的图象变换，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
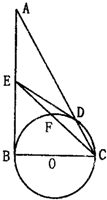（选修4-1）如图，在△ABC中，∠ABC=90°，以BC为直径的圆O交AC于点D，设E为AB的中点． 
+
x)+cos2πx-2cosπx.
与
的夹角.
+
x)+cos2πx-2cosπx.
与
的夹角.