题目内容
已知椭圆 ,F1,F2为两焦点,若椭圆上存在P,使得
,F1,F2为两焦点,若椭圆上存在P,使得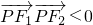 .则a,b满足的条件为
.则a,b满足的条件为
- A.
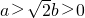
- B.
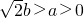
- C.
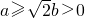
- D.
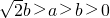
A
分析:首先根据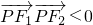 ?∠F1PF2是钝角,然后假设P处于(0,b)时有PF1⊥PF2,得出角是钝角时有2c>
?∠F1PF2是钝角,然后假设P处于(0,b)时有PF1⊥PF2,得出角是钝角时有2c> a,再根据c2=a2-b2即可求出结果.
a,再根据c2=a2-b2即可求出结果.
解答:∵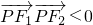
∴∠F1PF2是钝角,∠F1PF2在P处于(0,b)时最大,
假设P处于(0,b)时有PF1⊥PF2,此时2c= a,则角是钝角时有2c>
a,则角是钝角时有2c> a
a
即4c2>2a2,2c2>a2
即2(a2-b2)>a2
∴a2-2b2>0
∴a> b>0
b>0
故选A.
点评:本题考查了椭圆的简单性质,解题的关键是根据条件得出∠F1PF2是钝角,属于中档题.
分析:首先根据
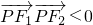 ?∠F1PF2是钝角,然后假设P处于(0,b)时有PF1⊥PF2,得出角是钝角时有2c>
?∠F1PF2是钝角,然后假设P处于(0,b)时有PF1⊥PF2,得出角是钝角时有2c> a,再根据c2=a2-b2即可求出结果.
a,再根据c2=a2-b2即可求出结果.解答:∵
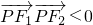
∴∠F1PF2是钝角,∠F1PF2在P处于(0,b)时最大,
假设P处于(0,b)时有PF1⊥PF2,此时2c=
 a,则角是钝角时有2c>
a,则角是钝角时有2c> a
a即4c2>2a2,2c2>a2
即2(a2-b2)>a2
∴a2-2b2>0
∴a>
 b>0
b>0故选A.
点评:本题考查了椭圆的简单性质,解题的关键是根据条件得出∠F1PF2是钝角,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
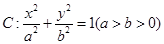 ,F1,F2为其左、右焦点,P为椭圆C上任一点,
,F1,F2为其左、右焦点,P为椭圆C上任一点,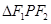 的重心为G,内心I,且有
的重心为G,内心I,且有 (其中
(其中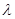 为实数),椭圆C的离心率e=( )
为实数),椭圆C的离心率e=( )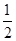 B.
B.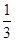 C.
C.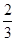 D.
D.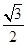
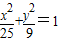 ,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )
,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )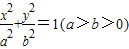 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .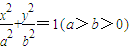 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .