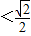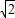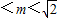题目内容
无论k取何实数,直线y=kx+m与圆(x-1)2+y2=2总有两个交点,则m的取值范围是
- A.-


- B.-1<m<1
- C.-
 <m
<m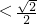
- D.-


B
分析:无论k取何实数,直线y=kx+m总是经过点A(0,m),由题意可得点A(0,m),在圆的内部,故有(0-1)2 +m2<2,由此求得m的取值范围.
解答:无论k取何实数,直线y=kx+m总是经过点A(0,m),再由直线y=kx+m与圆(x-1)2+y2=2总有两个交点,
可得点A(0,m),在圆的内部,(0-1)2 +m2<2,
∴-1<m<1,
故选B.
点评:本题主要考查直线和圆的位置关系,直线过定点问题,属于中档题.
分析:无论k取何实数,直线y=kx+m总是经过点A(0,m),由题意可得点A(0,m),在圆的内部,故有(0-1)2 +m2<2,由此求得m的取值范围.
解答:无论k取何实数,直线y=kx+m总是经过点A(0,m),再由直线y=kx+m与圆(x-1)2+y2=2总有两个交点,
可得点A(0,m),在圆的内部,(0-1)2 +m2<2,
∴-1<m<1,
故选B.
点评:本题主要考查直线和圆的位置关系,直线过定点问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

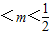
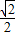 <m
<m