题目内容
已知直线l:(k-1)x+(2k+1)y=2k+1和圆C:(x-1)2+(y-2)2=16.
①求证:无论k取何值,直线l与圆C都相交;
②求直线l被圆C截得的弦长的最小值和弦长取得最小值时实数k的值.
答案:
解析:
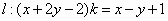 ,
,
 在圆
在圆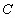 的内部,所以无论
的内部,所以无论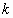 取何值,直线
取何值,直线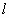 与圆
与圆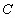 都相交 5分
都相交 5分
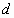 ,圆
,圆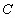 的半径为
的半径为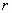 ,则
,则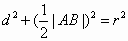 ,要使
,要使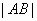 最小,当
最小,当 时,只需要
时,只需要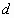 最大即可.又因为
最大即可.又因为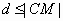 ,所以当
,所以当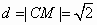 时,
时,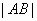 最小 8分
最小 8分
解析:
解:①因为直线![]()
由![]() 得
得![]() ,所以直线
,所以直线![]() 恒过定点
恒过定点![]()
又![]()
②设直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,圆心
两点,圆心![]() 到直线
到直线![]()
此时![]() ,所以
,所以![]() 9
9
当弦长![]() 时,直线
时,直线![]() .
.
又因为![]() ,所以直线
,所以直线![]() 的斜率
的斜率![]() 11
11
又![]() ,所以
,所以![]() 12
12

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知直线l:x=my+1过椭圆
如图,已知直线l:x=my+1过椭圆