Question

已知P是椭圆

x2

4

+

y2

3

=1上的一点，F₁、F₂是该椭圆的两个焦点，若△PF₁F₂的内切圆的半径为

1

2

，则tan∠F₁PF₂=（　　）

• A．

  3

  4

• B．

  4

  3

• C．

  4 7

  7

• D．

  3 7

  7

Answer 1

分析：作出图形，利用内切圆的性质与椭圆的定义及半角公式即可求得tan∠F₁PF₂的值．

解答：解：根据题意作图如下，设△PF₁F₂的内切圆心为M，则内切圆的半径|MQ|=

1

2

，设圆M与x轴相切于R，

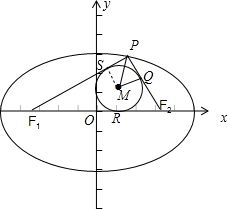
∵椭圆的方程为

x2

4

+

y2

3

=1，
∴椭圆的两个焦点F₁（-1，0），F₂（1，0），
∴|F₁F₂|=2，设|F₁R|=x，则|F₂R|=2-x，
依题意得，|F₁S|=|F₁R|=x，|F₂Q|=|F₂R|=2-x，
设|PS|=|PQ|=y，
∵|PF₁|=x+y，|PF₂|=（2-x）+y，|PF₁|+|PF₂|=4，
∴x+y+（2-x）+y=4，
∴y=1，即|PQ|=1，又|MQ|=

1

2

，MQ⊥PQ，
∴tan∠MPQ=

|MQ|

|PQ|

=

1 2

1

=

1

2

，
∴tan∠F₁PF₂=tan2∠MPQ=

2× 1 2

1-( 1 2 )2

=

4

3

．
故选B．

点评：本题考查椭圆的简单性质，考查内切圆的性质及半角公式，考查分析问题，通过转化思想解决问题的能力，属于难题．