题目内容
已知函数f（a）=
sinxdx，则f[f（
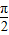）]=（ ）A．1
B．1-cos1
C．0
D．cos1-1
【答案】分析：先根据函数f（a）=
sinxdx计算f（
），再计算f[f（
）]即可．
解答：解：∵函数f（a）=
sinxdx，
∴f（
）=
sinxdx=-cosx 
=-1
∴f[f（
）]=f（-1）=-
sinxdx=cosx 
=1-cos1．
故选B．
点评：本题考查定积分的计算，考查复合函数的意义，正确求定积分是关键．
sinxdx计算f（），再计算f[f（）]即可．解答：解：∵函数f（a）=
sinxdx，∴f（
）=sinxdx=-cosx =-1∴f[f（
）]=f（-1）=-sinxdx=cosx =1-cos1．故选B．
点评：本题考查定积分的计算，考查复合函数的意义，正确求定积分是关键．
练习册系列答案
相关题目