题目内容
【题目】已知数列{an}的前n项和为Sn ， 且满足Sn=n2﹣4n，数列{bn}中，b1= 
对任意正整数 
．
（1）求数列{an}的通项公式；
（2）是否存在实数μ，使得数列{3nbn+μ}是等比数列？若存在，请求出实数μ及公比q的值，若不存在，请说明理由；
（3）求证： 
．
【答案】
（1）解：当n=1时，a1=S1=﹣3，
当n≥2时，an=Sn﹣Sn﹣1=n2﹣4n﹣（n﹣1）2+4（n﹣1），
即an=2n﹣5，
n=1也适合，所以an=2n﹣5
（2）解：法一：
假设存在实数μ，使数列{3nbn+μ}是等比数列，且公比为q．
因为对任意正整数 
， 
，
可令n=2，3，得 b2= 
，b3=﹣ 
．
因为{3nbn+μ}是等比数列，所以 
= 
，解得 μ=﹣ 
从而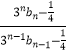 
= 
= 
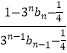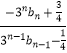=﹣3 （n≥2）
所以存在实数μ=﹣ ，公比为q=﹣3．
法二：因为对任意正整数 ．所以 
，
设3nbn+μ=﹣3（3n﹣1bn﹣1+μ），则﹣4μ=1，
所以存在 
，且公比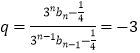 
（3）证明：因为a2=﹣1，a3=1，所以 ， 
，
所以 
，即 
，
于是b1+b2+…+bn= 
+ 
+ 
+… 
= 
= 
=
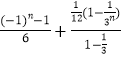当是奇数时：b1+b2+…+bn= 
，关于递增，
得 
≤b1+b2+…+bn＜ 
．
当是偶数时：b1+b2+…+bn= 
，关于递增，
得 
≤b1+b2+…+bn 
．
综上， ≤b1+b2+…+bn
【解析】（1）当n=1时，a1=S1=﹣3，当n≥2时，an=Sn﹣Sn﹣1 ， 可得an ． （2）法一：假设存在实数μ，使数列{3nbn+μ}是等比数列，且公比为q．因为对任意正整数 ， ，可令n=2，3，得 b2 ， b3 ． 根据{3nbn+μ}是等比数列，可得： = ，解得 μ，代入可得 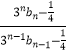=﹣3 （n≥2）即可证明． 法二：因为对任意正整数 ．所以 ，设3nbn+μ=﹣3（3n﹣1bn﹣1+μ），可得﹣4μ=1，即可证明．（3）由a2=﹣1，a3=1，可得 ， ，可得 ，即 ，利用等比数列的求和公式即可得出．对n分类讨论，利用数列的单调性即可证明．
