题目内容
(本小题满分14分)已知数列﹛ ﹜满足:
﹜满足: .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛ ﹜的通项公式;(Ⅱ)设
﹜的通项公式;(Ⅱ)设 ,求
,求
 ﹜满足:
﹜满足: .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛ ﹜的通项公式;(Ⅱ)设
﹜的通项公式;(Ⅱ)设 ,求
,求
(Ⅰ) ;(Ⅱ)
;(Ⅱ) 。
。
 ;(Ⅱ)
;(Ⅱ) 。
。试题分析:(Ⅰ)当
 时,
时, (1分)
(1分)当
 时,
时, ①
① ②
②①-②得
 ,所以
,所以 , (6分)
, (6分)经验证
 时也符合,所以
时也符合,所以 (7分)
(7分)(Ⅱ)
 ,则
,则 , (10分)
, (10分)所以
 , (12分)
, (12分)因此
 =
= (14分)
(14分)点评:通项公式及前n 项和的求解是数列的最基础的考查,是高考中的基础试题,对学生的要求是熟练掌握公式,并能进行一些基本运算.

练习册系列答案
相关题目
 是区域
是区域 ,(
,( )内的点,目标函数
)内的点,目标函数 ,
, 的最大值记作
的最大值记作 .若数列
.若数列 的前
的前 项和为
项和为 ,
,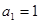 ,且点(
,且点( )在直线
)在直线 上.
上. 为等比数列;
为等比数列; 的前
的前 .
. 的通项公式是
的通项公式是 ,且
,且 ,则
,则 ( )
( ) 的前n项和为
的前n项和为 ,已知数列
,已知数列 是首项和公比都为3的等比数列,则数列
是首项和公比都为3的等比数列,则数列 =_____________________
=_____________________ 中,
中, ,则数列
,则数列 项的和为 .
项的和为 .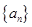 是等差数列,
是等差数列,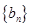 是各项为正数的等比数列,且
是各项为正数的等比数列,且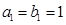 ,
,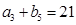 ,
,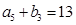 .
. 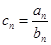 ,求数列
,求数列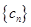 的前
的前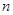 项和
项和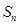 .
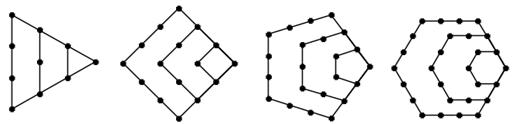
. 为“梯形数”.根据图形的构成,数列第
为“梯形数”.根据图形的构成,数列第 项
项 ; 第
; 第 项
项 .
. 
 ,将构图边数增加到
,将构图边数增加到 可得到“
可得到“ 项为
项为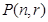 ,
,
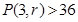 的最小
的最小 ,且
,且 ,则
,则 ( )
( )