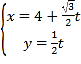题目内容
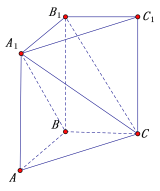
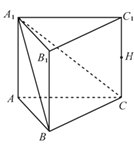
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 的中点为
的中点为![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() ;(Ⅲ)在棱
;(Ⅲ)在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.
【解析】
(Ⅰ)可证明![]() 平面
平面![]() ,从而得到
,从而得到![]() .
.
(Ⅱ)利用![]() ,
,![]() ,
,![]() 两两互相垂直建立如图所示空间直角坐标系
两两互相垂直建立如图所示空间直角坐标系![]() ,求出平面
,求出平面![]() 的法向量平面
的法向量平面![]() 的法向量后可求二面角的余弦值.
的法向量后可求二面角的余弦值.
(Ⅲ)设![]() ,则可用
,则可用![]() 表示
表示![]() ,利用
,利用![]() 与平面
与平面![]() 的法向量垂直可求
的法向量垂直可求![]() ,从而得到
,从而得到![]() 的值.
的值.
证明:(Ⅰ)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.

因为![]() ,所以
,所以![]() .
.
又因为![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.

(Ⅱ)由(Ⅰ)可知![]() ,
,![]() ,
,![]() 两两互相垂直,
两两互相垂直,
如图,建立空间直角坐标系![]() .
.
因为![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() 即为平面
即为平面![]() 的一个法向量.
的一个法向量.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,
则 即
即![]()
令![]() ,则
,则![]() .
.
于是![]() .
.
所以 .
.
由题知二面角![]() 为锐角,所以其余弦值为
为锐角,所以其余弦值为![]() .
.
(Ⅲ)假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() .
.
由![]() ,
,![]() 得
得![]() .
.
因为![]() ,
,![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
所以![]() .
.
若![]() 平面
平面![]() ,则
,则![]() ,解得
,解得![]() .
.
又因为![]() 平面
平面![]() .
.
所以在棱![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】东莞的轻轨给市民出行带来了很大的方便,越来越多的市民选择乘坐轻轨出行,很多市民都会开汽车到离家最近的轻轨站,将车停放在轻轨站停车场,然后进站乘轻轨出行,这给轻轨站停车场带来很大的压力.某轻轨站停车场为了解决这个问题,决定对机动车停车施行收费制度,收费标准如下:4小时内(含4小时)每辆每次收费5元;超过4小时不超过6小时,每增加一小时收费增加3元;超过6小时不超过8小时,每增加一小时收费增加4元,超过8小时至24小时内(含24小时)收费30元;超过24小时,按前述标准重新计费.上述标准不足一小时的按一小时计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间(假设每辆车一天内在该停车场仅停车一次),得到下面的频数分布表:
|
|
|
|
|
|
|
频数(车次) | 100 | 100 | 200 | 200 | 350 | 50 |
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率.
(1)现在用分层抽样的方法从上面1000辆车中抽取了100辆车进行进一步深入调研,记录并统计了停车时长与司机性别的![]() 列联表:
列联表:
男 | 女 | 合计 | |
不超过6小时 | 30 | ||
6小时以上 | 20 | ||
合计 | 100 |
完成上述列联表,并判断能否有90%的把握认为“停车是否超过6小时”与性别有关?
(2)(i)![]() 表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求
表示某辆车一天之内(含一天)在该停车场停车一次所交费用,求![]() 的概率分布列及期望
的概率分布列及期望![]() ;
;
(ii)现随机抽取该停车场内停放的3辆车,![]() 表示3辆车中停车费用大于
表示3辆车中停车费用大于![]() 的车辆数,求
的车辆数,求![]() 的概率.
的概率.
参考公式: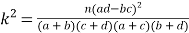 ,其中
,其中![]()
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】已知甲、乙两地生产同一种瓷器,现从两地的瓷器中随机抽取了一共300件统计质量指标值,得到如图的两个统计图,其中甲地瓷器的质量指标值在区间![]() 和
和![]() 的频数相等.
的频数相等.

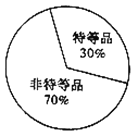
甲地瓷器质量频率分布直方图 乙地瓷器质量扇形统计图
(1)求直方图中![]() 的值,并估计甲地瓷器质量指标值的平均值;(同一组中的数据用区间的中点值作代表)
的值,并估计甲地瓷器质量指标值的平均值;(同一组中的数据用区间的中点值作代表)
(2)规定该种瓷器的质量指标值不低于125为特等品,且已知样本中甲地的特等品比乙地的特等品多10个,结合乙地瓷器质量扇形统计图完成下面的![]() 列联表,并判断是否有95%的把握认为甲、乙两地的瓷器质量有差异?
列联表,并判断是否有95%的把握认为甲、乙两地的瓷器质量有差异?
物等品 | 非特等品 | 合计 | |
甲地 | |||
乙地 | |||
合计 |
附: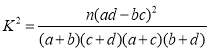 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |