题目内容
(1)设cos(α+β)=
,cos(α-β)=
,求cos2α+cos2β的值;
(2)已知α,β∈(
,π),sin(α+β)=-
,sin(β-
)=
,求cos(α+
)的值.
| ||
| 3 |
| ||
| 3 |
(2)已知α,β∈(
| 3π |
| 4 |
| 5 |
| 3 |
| π |
| 4 |
| 12 |
| 13 |
| π |
| 4 |
分析:(1)利用诱导公式和两角和与差公式进行化简即可.
(2)利用诱导公式和两角和与差公式进行化简即可.
(2)利用诱导公式和两角和与差公式进行化简即可.
解答:解:(1)cos(α+β)cos(α-β)=cos2αcos2β-sin2αsin2β
=cos2αcos2β-(1-cos2α)(1-cos2β)
=cos2αcos2β-1+cos2α+cos2β-cos2αcos2β
=
∴cos2α+cos2β=
…8分
(2)∵α,β∈(
,π)
∴
<2α+β<2π
<β-
<
∴cos(α+β)=
cos(β-
)=-
cos(α+
)=cos[(α+β)-(β-
)]
=cos(α+β)cos(β-
)+sin(α+β)sin(β-
)
=
×(-
)-
×
=-
…16分
=cos2αcos2β-(1-cos2α)(1-cos2β)
=cos2αcos2β-1+cos2α+cos2β-cos2αcos2β
=
| 1 |
| 9 |
∴cos2α+cos2β=
| 10 |
| 9 |
(2)∵α,β∈(
| 3π |
| 4 |
∴
| 3π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
∴cos(α+β)=
| 4 |
| 5 |
| π |
| 4 |
| 5 |
| 13 |
cos(α+
| π |
| 4 |
| π |
| 4 |
=cos(α+β)cos(β-
| π |
| 4 |
| π |
| 4 |
=
| 4 |
| 5 |
| 5 |
| 13 |
| 3 |
| 5 |
| 12 |
| 13 |
=-
| 56 |
| 65 |
点评:此题考查了诱导公式、两角和与差公式以及同角三角函数的基本关系,熟练掌握公式是解题的关键

练习册系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: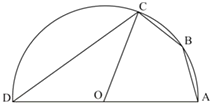 (2010•温州二模)设AD是半径为5的半圆O的直径(如图),B,C是半圆上两点,AB=BC=
(2010•温州二模)设AD是半径为5的半圆O的直径(如图),B,C是半圆上两点,AB=BC=