题目内容
【题目】已知椭圆
的离心率为
，其左、右焦点为F1、F2，点P是坐标平面内一点，且
其中O为坐标原点。
（I） 求椭圆C的方程；
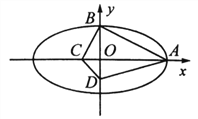
（II） 如图，过点S（0，
}，且斜率为k的动直线l交椭圆于A、B两点，在y轴上是否存在定点M，使以AB为直径的圆恒过这个点？若存在，求出点M的坐标；若不存在，请说明理由．
【答案】（1）
（2）在y轴上存在定点M，使得以AB为直径的圆恒过这个点，
点M的坐标为（0，1）。
【解析】
（1）利用
；（2）直线方程与椭圆方程，联立方程组并借助于韦达定理，求点的坐标.
解:(1)设
，
,
① ……1分
又,
，即
② ……2分
①代入②得：
. 又
故所求椭圆方程为
……4分
(2)设直线
，代入，有
.
设
，则
. ……6分
若
轴上存在定点
满足题设，则
，
，
……9分
由题意知，对任意实数
都有
恒成立， ……10分
即
对
成立.
解得
， ……11分
在轴上存在定点
,使以
为直径的圆恒过这个定点. ……12分
练习册系列答案
相关题目
