题目内容
求函数y＝sin(2x＋
)的最小正周期及y＝｜sin(2x＋)｜的最小正周期．
答案：
解析：
提示：
解析：
|
解：(1)y＝sin(2x＋ (2)∵f(x＋ ＝｜－sin(2x＋ ∴T＝ 假设存在0＜T＜ 令x＝0，有｜sin( ∵0＜T＜ ∴sin( 从而对任意x应有sin(2x＋ 与当x＝ ∴T＝ |
)的最小正周期T＝
＝
＝π．
)＝｜sin［2(x＋
．
．
∴T＝0(舍去)或
时，sinπ≠sin提示：
|
反证法是证明最小正周期的常用办法，举反例时，只要有一则反例即可．另外，本单元第三节将介绍y＝Asin(ωx＋φ)的图象，到时可以借助图象直接观察出y＝｜sin(2x＋ |
练习册系列答案
相关题目
)，x∈[－2π，2π]的单调增区间．
]，求函数y＝sinα＋
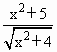最小值；
的最小值；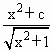
(c＞0)，求函数的最小值．
.
sin 2x)，函数f(x)＝p·q－5(a∈R，a≠0)