题目内容
求函数y=sin(![]() ),x∈[-2π,2π]的单调增区间.
),x∈[-2π,2π]的单调增区间.
答案:
解析:
解析:
|
解:y=sin( 由于y=sinx与y=-sinx的图象关于x轴对称可知,y=sinx的增区间就是y=-sinx的减区间.因此,要求y=-sin( 令z= 得 取k=-1,得 又∵x∈[-2π,2π], ∴y=sin( |

练习册系列答案
相关题目
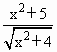 的最小值;
的最小值;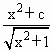 (c>0),求函数的最小值.
(c>0),求函数的最小值.