题目内容
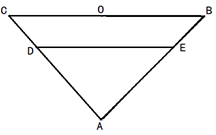
如图,在等腰直角三角形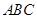 中,
中, 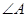 =900 ,
=900 ,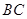 ="6,"
="6," 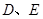 分别是
分别是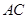 ,
,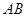 上的点,
上的点,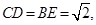
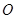 为
为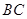 的中点.将
的中点.将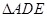 沿
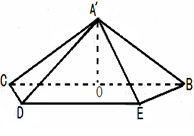
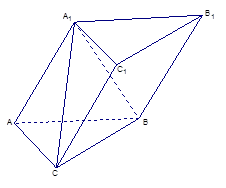
沿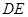 折起,得到如图所示的四棱椎
折起,得到如图所示的四棱椎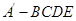 ,其中
,其中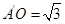
(1)证明: ;
;
(2)求二面角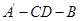 的平面角的余弦值.
的平面角的余弦值.
(1)详见解析 (2)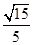
解析试题分析:(1)F为ED的中点,连接OF,A’F,根据已知计算出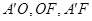 的长度,满足勾股定理,
的长度,满足勾股定理,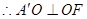 , A’F为等腰△A’DE底边的中线,
, A’F为等腰△A’DE底边的中线,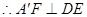 ,
,  ,证得线面垂直,线线垂直,再线面垂直;(2)过点O作
,证得线面垂直,线线垂直,再线面垂直;(2)过点O作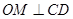 的延长线于
的延长线于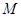 ,连接
,连接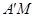 .利用(1)可知:
.利用(1)可知: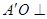 平面
平面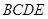 ,根据三垂线定理得
,根据三垂线定理得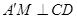 ,所以
,所以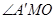 为二面角
为二面角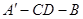 的平面角.在直角
的平面角.在直角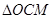 中,求出
中,求出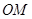 即可;
即可;
试题解析:
证明: (1)设F为ED的中点,连接OF,A’F,计算得A’F=2,OF=1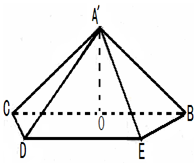
∵A’F为等腰△A’DE底边的中线,∴A’F⊥DE
∵OF在原等腰△ABC底边BC的高线上,
∴OF⊥DE
又∵A’F,OF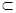 平面A’OF, A’F
平面A’OF, A’F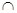 OF=F,
OF=F,
∴DE⊥平面A’OF
∵A’O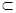 平面A’OF, ∴DE⊥A’O
平面A’OF, ∴DE⊥A’O
在△A’FO中,A’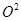 +
+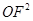 =3+1=
=3+1=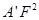 ,∴A’O⊥OF
,∴A’O⊥OF
∵OF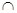 DE=F,OF
DE=F,OF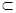 平面BCDE,DE
平面BCDE,DE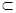 平面BCDE, ∴A’O⊥平面BCDE 6分
平面BCDE, ∴A’O⊥平面BCDE 6分
(2):如答图1,过O作CD的垂线交CD的延长线于M,连接A’M
∵A’O⊥平面BCDE,CD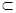 平面BCDE, ∴CD⊥A’O ∵OM
平面BCDE, ∴CD⊥A’O ∵OM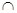 A’O="O," ∴CD⊥平面A’OM
A’O="O," ∴CD⊥平面A’OM
∵A’M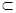 平面A’OM∴CD⊥A’M ∴
平面A’OM∴CD⊥A’M ∴ ∠A’MO为所求二面角的平面角
∠A’MO为所求二面角的平面角
在Rt△OMC中,OM=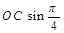 =
=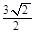 , A’O=
, A’O=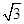 于是在Rt△A’OM中,A’M=
于是在Rt△A’OM中,A’M=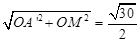 ∴
∴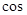 ∠A’OM=
∠A’OM=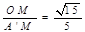 13分
13分
考点:1.线面垂直的判定;2.二面角的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 AB.Q是PC上的一点.
AB.Q是PC上的一点.
 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
 平面
平面 ;
; 的大小;
的大小; 与平面
与平面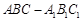 中,侧面
中,侧面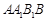 为菱形, 且
为菱形, 且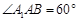 ,
,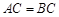 ,
,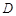 是
是 的中点.
的中点.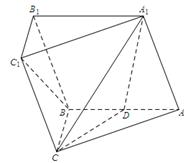
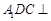 平面
平面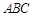 ;
;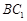 ∥平面
∥平面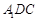 .
. ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点
ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点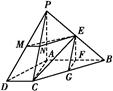
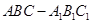 中,D、E分别是BC和
中,D、E分别是BC和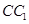 的中点,已知AB=AC=AA1=4,ÐBAC=90°.
的中点,已知AB=AC=AA1=4,ÐBAC=90°.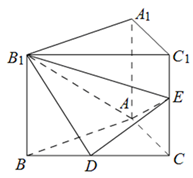
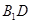 ⊥平面
⊥平面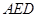 ;
;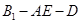 的余弦值;
的余弦值;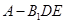 的体积.
的体积.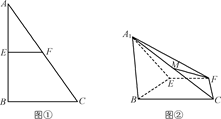
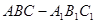 中,四边形
中,四边形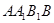 是菱形,四边形
是菱形,四边形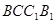 是矩形,
是矩形,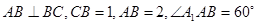 .
.
 ;
;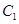 到平面
到平面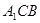 的距离;
的距离;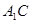 与平面
与平面