题目内容
实数x，y满足，x-y≥0，x+y≤1，x+2y≥1，则z=6x+3y的最小值为
3
3
．分析：先利用二元一次不等式表示平面区域的性质画出线性约束条件对应的可行域，再将目标函数赋予几何意义，数形结合得最优解，代入目标函数即可得目标函数的最值
解答：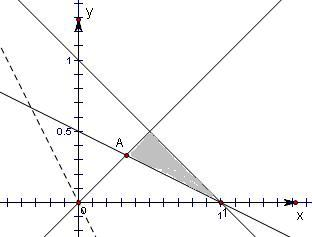
解：画出可行域如图阴影区域：
由x+y=1及x+2y=1，得A（
，
）
目标函数z=6x+3y可看做斜率为-2的动直线l，由图数形结合可知：
当l过点A时，z最小为6×
+3×
=3．
故答案为3．
解：画出可行域如图阴影区域：由x+y=1及x+2y=1，得A（
| 1 |
| 3 |
| 1 |
| 3 |
目标函数z=6x+3y可看做斜率为-2的动直线l，由图数形结合可知：
当l过点A时，z最小为6×
| 1 |
| 3 |
| 1 |
| 3 |
故答案为3．
点评：本题主要考查了简单线性规划问题的一般解法，线性约束条件对应的可行域的画法，数形结合解决问题的思想方法，属基础题
练习册系列答案
相关题目
的函数f(x)对任意实数x，y满足f(x＋y)＋f(x－y)＝2f(x)cosy，且f(0)＝0，
，给出下列结论：①
；②f(x)为奇函数；③f(x)是周期函数；④f(x)在(0，π)内为单调函数