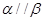题目内容
设 、
、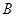 两点的坐标分别为
两点的坐标分别为 、
、 ,条件甲:点
,条件甲:点 满足
满足 ; 条件乙:点
; 条件乙:点 的坐标是方程
的坐标是方程 的解. 则甲是乙的( )
的解. 则甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不是充分条件也不是必要条件 |
B
解析试题分析:设 ,条件甲:
,条件甲: .其对应的图形是圆内,而点
.其对应的图形是圆内,而点 的坐标是方程
的坐标是方程 的解的点
的解的点 所对应的图形是椭圆,观察图形得甲是乙的必要不充分条件即可.
所对应的图形是椭圆,观察图形得甲是乙的必要不充分条件即可.
考点:必要条件、充分条件与充要条件的判断;数量积表示两个向量的夹角.

练习册系列答案
相关题目
命题“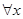 ∈R,
∈R,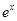 -x+1≥0”的否定是( )
-x+1≥0”的否定是( )
A.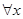 ∈R,lnx+x+1<0 ∈R,lnx+x+1<0 | B.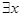 ∈R, ∈R,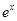 -x+1<0 -x+1<0 |
C.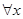 ∈R, ∈R,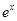 -x+1>0 -x+1>0 | D.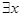 ∈R, ∈R,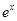 -x+1≥0 -x+1≥0 |
设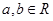 ,则“
,则“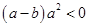 ”是“
”是“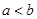 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若“0<x<1”是“(x-a)[x-(a+2)]≤0”的充分不必要条件,则实数a的取值范围是( )
| A.(-∞,0]∪[1,+∞) | B.(-1,0) |
| C.[-1,0] | D.(-∞,-1)∪(0,+∞) |
命题“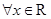 ,
,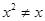 ”的否定是( )
”的否定是( )
A.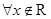 , ,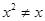 | B.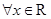 , ,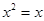 |
C.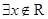 , ,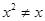 | D.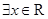 , ,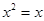 |
已知条件 :
: ,条件
,条件 :
: ,则
,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既非充分也非必要条件 |
设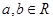 ,则“
,则“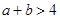 ”是“
”是“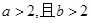 ”的( )
”的( )
| A.充分条件 | B.必要条件 |
| C.充分必要条件 | D.既非充分又非必要条件 |
[2012·浙江高考]设a∈R,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分又不必要条件 |
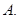 若
若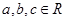 ,则
,则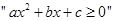 的充分条件是
的充分条件是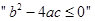
 若
若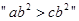 的充要条件是
的充要条件是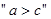
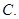 命题“对任意
命题“对任意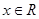 ,有
,有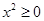 ”的否定是“存在
”的否定是“存在
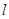 是一条直线,
是一条直线,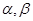 是两个不同的平面,若
是两个不同的平面,若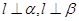 ,则
,则