题目内容
下列叙述中正确的是( )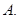 若
若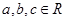 ,则
,则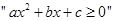 的充分条件是
的充分条件是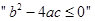
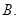 若
若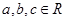 ,则
,则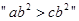 的充要条件是
的充要条件是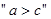
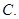 命题“对任意
命题“对任意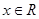 ,有
,有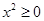 ”的否定是“存在
”的否定是“存在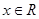 ,有
,有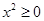 ”
”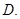
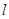 是一条直线,
是一条直线,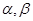 是两个不同的平面,若
是两个不同的平面,若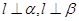 ,则
,则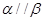
D
解析试题分析:当 时,
时,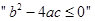 推不出
推不出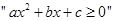 ,
,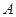 错,当
错,当 时,
时,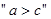 推不出
推不出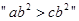 ,
,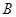 错,命题“对任意
错,命题“对任意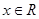 ,有
,有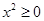 ”的否定是“存在
”的否定是“存在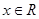 ,有
,有 ”,C错,因为与同一直线垂直的两平面平行,所以D正确.
”,C错,因为与同一直线垂直的两平面平行,所以D正确.
考点:充要关系

练习册系列答案
相关题目
函数 有极值的充要条件是 ( )
有极值的充要条件是 ( )
A. | B. | C. | D. |
命题“存在 ”的否定是( )
”的否定是( )
A.存在 | B.不存在 |
C.对任意 | D.对任意 |
下列四个命题: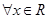 ,
,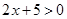 ”是全称命题;
”是全称命题;
命题“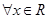 ,
,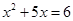 ”的否定是“
”的否定是“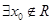 ,使
,使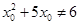 ”;
”;
若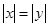 ,则
,则 ;
;
若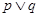 为假命题,则
为假命题,则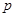 、
、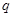 均为假命题.
均为假命题.
其中真命题的序号是( )
| A.①② | B.①④ | C.②④ | D.①②③④ |
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数 都满足:
都满足: 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”.已知函数
的“隔离直线”.已知函数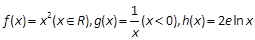 .有下列命题:
.有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”, 且b的最小值为-4;
之间存在“隔离直线”, 且b的最小值为-4;
③ 和
和 之间存在“隔离直线”, 且k的取值范围是
之间存在“隔离直线”, 且k的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( ).
| A.1个 | B.2个 | C.3个 | D.4个 |
设 、
、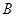 两点的坐标分别为
两点的坐标分别为 、
、 ,条件甲:点
,条件甲:点 满足
满足 ; 条件乙:点
; 条件乙:点 的坐标是方程
的坐标是方程 的解. 则甲是乙的( )
的解. 则甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不是充分条件也不是必要条件 |
函数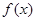 在
在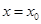 处导数存在,若
处导数存在,若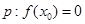 ;
;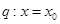 是
是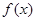 的极值点,则( )
的极值点,则( )
A.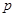 是 是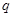 的充分必要条件 的充分必要条件 |
B.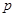 是 是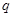 的充分条件,但不是 的充分条件,但不是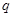 的必要条件 的必要条件 |
C.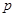 是 是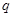 的必要条件,但不是 的必要条件,但不是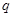 的充分条件 的充分条件 |
D.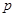 既不是 既不是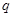 的充分条件,也不是 的充分条件,也不是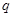 的必要条件 的必要条件 |
“a=-1”是“直线a2x-y+6=0与直线4x-(a-3)y+9=0互相垂直”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题p:对?x∈R,?m∈R,使4x+2xm+1=0.若命题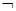 p是假命题,则实数m的取值范围是( )
p是假命题,则实数m的取值范围是( )
| A.[-2,2] | B.[2,+∞) |
| C.(-∞,-2] | D.[-2,+∞) |