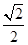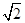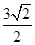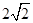题目内容
过抛物线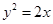 的焦点
的焦点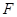 作直线
作直线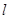 交抛物线于
交抛物线于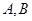 两点,若
两点,若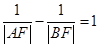 ,则直线
,则直线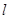 的倾斜角
的倾斜角 。
。
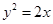 的焦点
的焦点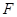 作直线
作直线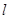 交抛物线于
交抛物线于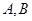 两点,若
两点,若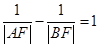 ,则直线
,则直线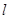 的倾斜角
的倾斜角 。
。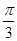 或
或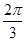
试题分析:由题意可得:F(
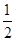 ,0)设A(x1,y1),B(x2,y2).因为过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点,所以|AF|=
,0)设A(x1,y1),B(x2,y2).因为过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点,所以|AF|=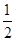 +x1,|BF|=
+x1,|BF|=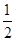 +x2.又因为
+x2.又因为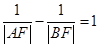 ,所以|AF|<|BF|,即x1<x2,并且直线l的斜率存在.设直线l的方程为y=k(x-
,所以|AF|<|BF|,即x1<x2,并且直线l的斜率存在.设直线l的方程为y=k(x-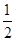 ),联立直线与抛物线的方程可得:k2x2-(k2+2)x+
),联立直线与抛物线的方程可得:k2x2-(k2+2)x+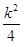 =0,所以x1+x2=
=0,所以x1+x2=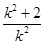 ,x1x2=
,x1x2=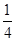 .因为
.因为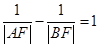 ,所以整理可得
,所以整理可得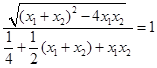 ,即整理可得k4-2k2-3=0,所以解得k2=3.因为0<θ≤
,即整理可得k4-2k2-3=0,所以解得k2=3.因为0<θ≤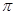 ,所以k=
,所以k=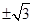 ,即θ=
,即θ=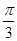 或
或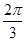
点评:解决此类问题的关键是熟练掌握抛物线的定义,以及掌握直线与抛物线位置关系,并且结合准确的运算也是解决此类问题的一个重要方面

练习册系列答案
相关题目
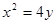 的焦点为
的焦点为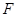 ,过
,过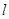 (
(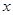 轴不平行)交抛物线分别于
轴不平行)交抛物线分别于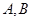 两点,点
两点,点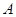 关于
关于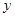 轴对称点为
轴对称点为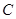 ,
,
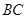 与
与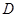 必为定点;
必为定点;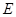 ,求
,求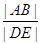 的最小值,并求当
的最小值,并求当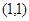 的抛物线的标准方程是 .
的抛物线的标准方程是 .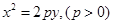 焦点为
焦点为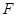 ,过
,过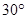 的直线,与抛物线交于A,B两点,若
的直线,与抛物线交于A,B两点,若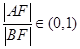 ,则
,则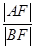 = ( )
= ( )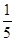
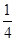

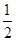
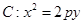 (
(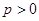 )上一点
)上一点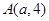 到其准线的距离为
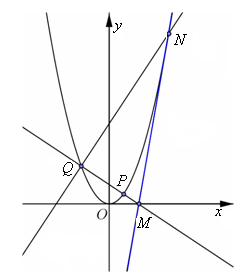
到其准线的距离为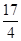 .
.
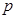 与
与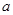 的值;
的值;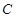 上动点
上动点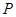 的横坐标为
的横坐标为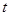 (
(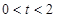 ),过点
),过点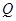 ,交
,交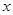 轴于
轴于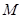 点(直线
点(直线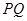 的斜率记作
的斜率记作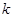 ).过点
).过点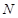 .若
.若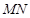 恰好是
恰好是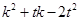 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由. ,则抛物线方程是( )
,则抛物线方程是( )



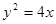 及点
及点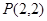 ,直线
,直线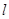 的斜率为1且不过点P,与抛物线交于A,B两点。
的斜率为1且不过点P,与抛物线交于A,B两点。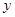 轴上截距的取值范围;
轴上截距的取值范围;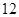 点时,拱顶离水面
点时,拱顶离水面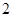 米,桥下的水面宽
米,桥下的水面宽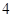 米;下午
米;下午 米,桥下的水面宽 米.
米,桥下的水面宽 米.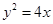 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于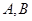 两点,点
两点,点 是原点,若
是原点,若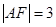 ,则
,则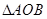 的面积为( )
的面积为( )