题目内容
已知抛物线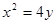 的焦点为
的焦点为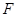 ,过
,过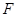 任作直线
任作直线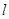 (
(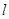 与
与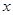 轴不平行)交抛物线分别于
轴不平行)交抛物线分别于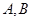 两点,点
两点,点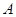 关于
关于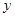 轴对称点为
轴对称点为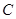 ,
,
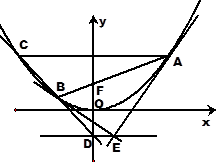
(1)求证:直线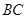 与
与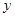 轴交点
轴交点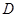 必为定点;
必为定点;
(2)过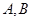 分别作抛物线的切线,两条切线交于
分别作抛物线的切线,两条切线交于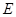 ,求
,求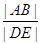 的最小值,并求当
的最小值,并求当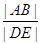 取最小值时直线
取最小值时直线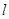 的方程.
的方程.
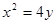 的焦点为
的焦点为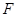 ,过
,过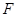 任作直线
任作直线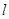 (
(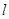 与
与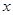 轴不平行)交抛物线分别于
轴不平行)交抛物线分别于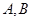 两点,点
两点,点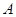 关于
关于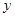 轴对称点为
轴对称点为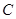 ,
,
(1)求证:直线
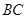 与
与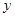 轴交点
轴交点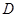 必为定点;
必为定点;(2)过
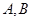 分别作抛物线的切线,两条切线交于
分别作抛物线的切线,两条切线交于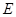 ,求
,求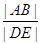 的最小值,并求当
的最小值,并求当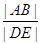 取最小值时直线
取最小值时直线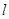 的方程.
的方程.(1)通过确定直线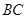 的方程,证明直线
的方程,证明直线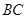 与
与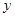 轴交于定点
轴交于定点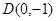 .
.
(2)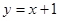 或
或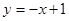 .
.
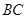 的方程,证明直线
的方程,证明直线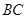 与
与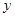 轴交于定点
轴交于定点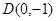 .
.(2)
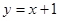 或
或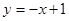 .
.试题分析:(1)通过确定直线
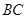 的方程,证明直线
的方程,证明直线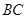 与
与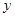 轴交于定点
轴交于定点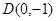 .
.(2)应用导数的几何意义,确定过点
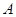 及过点
及过点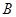 的切线方程并联立方程组,确定
的切线方程并联立方程组,确定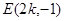 ,
,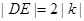 ,
,进一步应用“弦长公式”及均值定理,建立
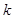 的方程,确定得到
的方程,确定得到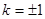 ,从而求得直线
,从而求得直线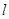 的方程为:
的方程为: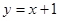 或
或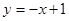 .
.试题解析:设
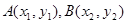 ,∵抛物线
,∵抛物线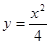 的焦点为
的焦点为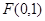
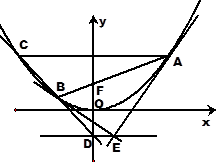
∴可设直线
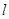 的方程为:
的方程为: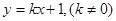
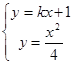 ,消去
,消去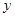 并整理得:
并整理得: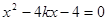
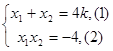 4分
4分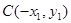 ,
,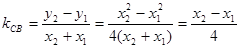
直线
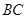 的方程为
的方程为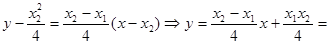
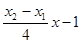
∴直线
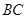 与
与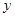 轴交于定点
轴交于定点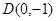 7分
7分(2)
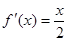 ,∴过点
,∴过点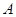 的切线方程为:
的切线方程为: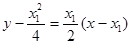
即:
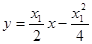 ③,同理可得过点
③,同理可得过点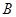 的切线方程为:
的切线方程为: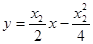 ④ 9分
④ 9分③—④得:
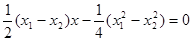 (
(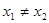 )
)∴
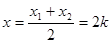
③+④得:
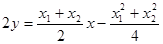
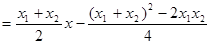
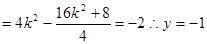 12分
12分∴
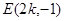 ,
,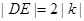
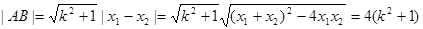
∴
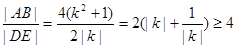 ,取等号时,
,取等号时,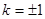 ,
,直线
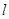 的方程为:
的方程为: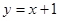 或
或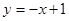 . 15分
. 15分
练习册系列答案
相关题目
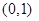 ,且在x轴上截得弦长为2,记该圆圆心的轨迹为E.
,且在x轴上截得弦长为2,记该圆圆心的轨迹为E.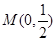 的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为
的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为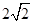 时,求直线m的方程.
时,求直线m的方程.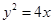 的焦点为
的焦点为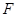 ,准线为直线
,准线为直线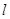 ,过抛物线上一点
,过抛物线上一点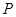 作
作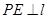 于
于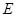 ,若直线
,若直线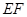 的倾斜角为
的倾斜角为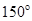 ,则
,则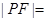 ______.
______. 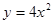 的焦点坐标是( )
的焦点坐标是( )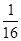 )
) 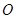 为坐标原点,
为坐标原点,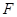 为抛物线
为抛物线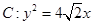 的焦点,
的焦点,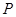 为
为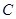 上一点,若
上一点,若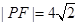 ,则
,则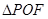 的面积为( )
的面积为( )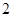
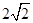
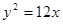 的焦点为
的焦点为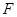 ,点
,点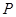 为抛物线上的动点,点
为抛物线上的动点,点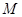 为其准线上的动点,当
为其准线上的动点,当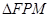 为等边三角形时,则
为等边三角形时,则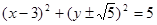
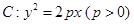 ,直线
,直线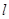 过抛物线
过抛物线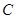 的焦点
的焦点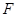 ,且与
,且与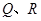 两点,
两点, 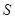 为
为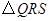 的面积为
的面积为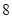 ,则
,则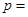 ( )
( )
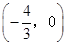
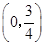
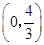
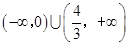
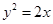 的焦点
的焦点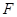 作直线
作直线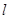 交抛物线于
交抛物线于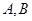 两点,若
两点,若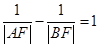 ,则直线
,则直线 。
。