题目内容
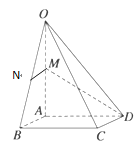
【题目】已知，如图， 
，图中的一系列圆是圆心分别为
， 
的两组同心圆，每组同心圆的半径依次为
， 
， 
，
按“加
”依次递增，点
是某两圆的一个交点，设：
以
， 
为焦点，且过点
的椭圆为
；
以
， 
为焦点，且过点
的双曲线为
，
则
（
）双曲线
离心率
__________．
（
）若以
为
轴正方向，线段
中点为坐标原点建立平面直角坐标系，则
椭圆
方程为__________．
（3）双曲线
渐近线方程为__________．
（4）在两组同心圆的交点中，在椭圆
上的点共__________个．
【答案】 （1）
（2）
（3）
（4）
【解析】（1）由图可知，
在双曲线
中
，
其离心率
，
（2）（i）在椭圆
中， 
，
∴
，
∴椭圆
的方程为
，
（ii）∵双曲线
的方程为
，
双曲线
的渐近线方程为
，
（3）∵椭圆
上的各点到
、
的距离之和为定理
．
由图可知共
个点满足题意．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
