题目内容
如图:在三棱锥![]() 中,
中,![]()
![]() 是直角三角形,
是直角三角形,
![]() ,
,![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(Ⅲ)求二面角![]() 的正切值.
的正切值.
解法一:(Ⅰ) 连结BD.在![]() 中,
中,![]() .
.

∵![]() ,点
,点![]() 为AC的中点,∴
为AC的中点,∴![]() .
.
又∵![]() 即BD为PD在平面ABC内的射影,
即BD为PD在平面ABC内的射影,
∴![]() .
.
∵![]() 分别为
分别为![]() 的中点,∴
的中点,∴![]() ,
,
∴![]() .
.
(Ⅱ)∵![]() ∴
∴![]() .
.
连结![]() 交
交![]() 于点
于点![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,
所成的角,![]() .
.
∵![]() ∴
∴![]() ,
,![]() ,又∵
,又∵![]() ,
,
∴![]() .∵
.∵![]() ,∴
,∴![]() ,
,
∴在Rt△![]() 中,
中,![]() ,∴
,∴![]() .
.
(Ⅲ)过点![]() 作
作![]() 于点F,连结
于点F,连结![]() ,∵
,∵![]()
∴![]() 即BM为EM在平面PBC内的射影,
即BM为EM在平面PBC内的射影,
∴![]() ∴
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
∵![]() 中,
中,![]() ,∴
,∴![]() .
.
解法二:建立空间直角坐标系B―xyz,如图,

则![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)∵![]() ,
,![]() ,
,
∴![]() ∴
∴![]() .
.
(Ⅱ)由已知可得,![]() 为平面
为平面![]() 的法向量,
的法向量,
![]() ,
,
∴  ,
,
∴直线![]() 与面
与面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
∴直线![]() 与面
与面![]() 所成的角为
所成的角为![]() .
.
(Ⅲ)设平面PEF的一个法向量为a![]() ,∵
,∵![]() ,
,![]()
∴![]() 令
令![]() ,∴ a
,∴ a![]()
由已知可得,向量![]() 为平面PBF的一个法向量,
为平面PBF的一个法向量,
∴ ![]() a
a  ,∴
,∴![]() a
a ![]() .
.
∴二面角![]() 的正切值为
的正切值为![]() .
.

练习册系列答案
相关题目
 如图,在三棱锥
如图,在三棱锥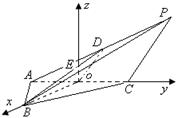

 (Ⅱ)求直线
(Ⅱ)求直线