题目内容
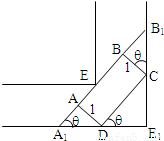
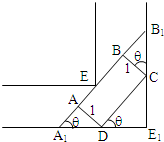 一条直角走廊宽 1.5米,如图所示,现有一转动灵活的手推车,其平板面为矩形ABCD,宽AD为1米,延长AB交直角走廊于A1、B1,设∠CDE1=θ,
一条直角走廊宽 1.5米,如图所示,现有一转动灵活的手推车,其平板面为矩形ABCD,宽AD为1米,延长AB交直角走廊于A1、B1,设∠CDE1=θ,(1)证明:A1B1=1.5(
| 1 |
| sinθ |
| 1 |
| cosθ |
(2)求A1B1的最小值.
分析:(1)由已知中直角走廊宽为1.5m,转动灵活的平板手推车,宽为1m,我们设AB所在直线与走廊外轮廓线交于点A1、B1,根据A1B 1=A1O+OB1,可证;
(2)利用导数法,判断出函数的单调性,及最值,即可得到答案.
(2)利用导数法,判断出函数的单调性,及最值,即可得到答案.
解答:解:(1)由题意A1B 1=A1O+OB1,
∵一条直角走廊宽 1.5米,∠CDE1=θ,
∴A′B′=
+
,
(2)求导函数得A1B1 /=1.5×
令导数为0,可得tanθ=1,∴θ=
又函数在(0,
)上单调减,在(
,
)上单调增
∴θ=
时幂函数取极小值,且为最小值
此时A1B1的最小值为3
∵一条直角走廊宽 1.5米,∠CDE1=θ,
∴A′B′=
| 1.5 |
| sinθ |
| 1.5 |
| cosθ |
(2)求导函数得A1B1 /=1.5×
| sin3θ-cos3θ |
| sin2θcos2θ |
令导数为0,可得tanθ=1,∴θ=
| π |
| 4 |
又函数在(0,
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴θ=
| π |
| 4 |
此时A1B1的最小值为3
| 2 |
点评:本题的考查的知识点是利用导研究函数的单调性,函数模型的选择,利用导数求闭区间上的函数的最值,其中将实际问题转化为利用导数法求函数最值问题,是解答本题的关键.

练习册系列答案
相关题目
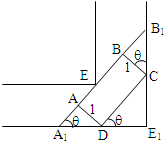 (理科)一条直角走廊宽 1.5米,如图所示,现有一转动灵活的手推车,其平板面为矩形ABCD,宽AD为1米,延长AB交直角走廊于A1、B1,设∠CDE1=θ,
(理科)一条直角走廊宽 1.5米,如图所示,现有一转动灵活的手推车,其平板面为矩形ABCD,宽AD为1米,延长AB交直角走廊于A1、B1,设∠CDE1=θ,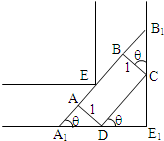 (理科)一条直角走廊宽 1.5米,如图所示,现有一转动灵活的手推车,其平板面为矩形ABCD,宽AD为1米,延长AB交直角走廊于A1、B1,设∠CDE1=θ,
(理科)一条直角走廊宽 1.5米,如图所示,现有一转动灵活的手推车,其平板面为矩形ABCD,宽AD为1米,延长AB交直角走廊于A1、B1,设∠CDE1=θ,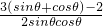 .
.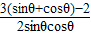 .
.
 +
+ ).
).