题目内容
如图，已知：平面α∥平面β，A、C∈α，B、D∈β，AC与BD为异面直线，AC=6，BD=8，AB=CD=10，AB与CD成60°的角，求AC与BD所成的角．考点：异面直线及其所成的角
专题：空间角
分析：在β内过D做DE∥AC，DE=AC，连接AE，BE，得到平行四边形AEDC，在三角形BDE中，利用勾股定理得到∠EDB为90°，即AC与BD所成的角为90°．
解答：
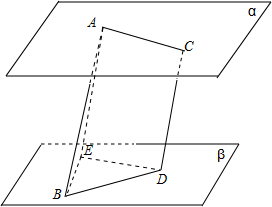解：如图，
在β内过D做DE∥AC，DE=AC，连接AE，BE，
∴∠EDB就是直线AC与BD所成角，
∵DE∥AC，DE=AC，
∴四边形AEDC为平行四边形，
∴AE∥CD，因此∠BAE为AB与CD所成的角，等于60°，
又AB=CD=10，
∴AB=AE=10，
∴△ABE为正三角形，
∴BE=10，
又BD=8，AC=6．
∴BD2+DE2=BE2．
则∠EDB=90°．
即直线AC与BD所成角为90°．
解：如图，在β内过D做DE∥AC，DE=AC，连接AE，BE，
∴∠EDB就是直线AC与BD所成角，
∵DE∥AC，DE=AC，
∴四边形AEDC为平行四边形，
∴AE∥CD，因此∠BAE为AB与CD所成的角，等于60°，
又AB=CD=10，
∴AB=AE=10，
∴△ABE为正三角形，
∴BE=10，
又BD=8，AC=6．
∴BD2+DE2=BE2．
则∠EDB=90°．
即直线AC与BD所成角为90°．
点评：本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力，关键是找到两条异面直线所成的角，是中档题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
已知函数f（x）=2（x-a）（x-b）（其中a＞b）的图象如右图，则函数g（x）=ax+b的图象一定不过第